题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,E为线段
,E为线段![]() 的中点.
的中点.
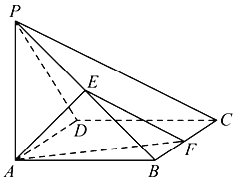
(1)证明:点F在线段![]() 上移动时,
上移动时,![]() 为直角三角形;
为直角三角形;
(2)若F为线段![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)利用等腰三角形的性质可得:![]() ,再利用线面垂直的性质定理判定定理及其正方形的性质可得:
,再利用线面垂直的性质定理判定定理及其正方形的性质可得:![]() 平面
平面![]() ,进而证明
,进而证明![]() 平面
平面![]() ,即可得出结论.
,即可得出结论.
(2)由题意,以![]() ,
,![]() ,
,![]() 所在直线分别为x,y,z轴建立空间直角坐标系,令
所在直线分别为x,y,z轴建立空间直角坐标系,令![]() ,易知平面
,易知平面![]() 的一个法向量为
的一个法向量为![]() .设平面
.设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,可得:
,可得:![]() .利用向量夹角公式即可得出.
.利用向量夹角公式即可得出.
(1)证明:因为![]() ,E为线段
,E为线段![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为底面![]() 为正方形,所以
为正方形,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以点F在线段![]() 上移动时,
上移动时,![]() 为直角三角形.
为直角三角形.
(2)由题意,以![]() ,
,![]() ,
,![]() 所在直线分别为x,y,z轴建立空间直角坐标系,令
所在直线分别为x,y,z轴建立空间直角坐标系,令![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
易知平面![]() 的一个法向量为
的一个法向量为![]() ;
;
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,可得:
,可得:![]() ,
,![]() ,
,
取![]() ,
,
所以![]() ,
,
由图可知:二面角![]() 的平面角为钝角,因此余弦值为
的平面角为钝角,因此余弦值为![]() .
.


练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
【题目】《周易》历来被人们视作儒家群经之首,它表现了古代中华民族对万事万物的深刻而又朴素的认识,是中华人文文化的基础,它反映出中国古代的二进制计数的思想方法.我们用近代术语解释为:把阳爻“- ”当作数字“1”,把阴爻“--”当作数字“0”,则八卦所代表的数表示如下:
卦名 | 符号 | 表示的二进制数 | 表示的十进制数 |
坤 |
| 000 | 0 |
震 |
| 001 | 1 |
坎 |
| 010 | 2 |
兑 |
| 011 | 3 |
依此类推,则六十四卦中的“屯”卦,符号“![]() ”表示的十进制数是( )
”表示的十进制数是( )
A. 18B. 17C. 16D. 15