题目内容
在直角坐标系xOy中,中心在原点O,焦点在x轴上的椭圆C上的点(2 ,1)到两焦点的距离之和为4
,1)到两焦点的距离之和为4 .
.
(1)求椭圆C的方程;
(2)过椭圆C的右焦点F作直线l与椭圆C分别交于A,B两点,其中点A在x轴下方,且 =3
=3 .求过O,A,B三点的圆的方程.
.求过O,A,B三点的圆的方程.
(1)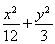 =1(2)x2+y2-
=1(2)x2+y2-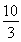 x-
x-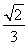 y=0.
y=0.
【解析】(1)由题意,设椭圆C: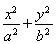 =1(a>b>0),则2a=4
=1(a>b>0),则2a=4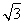 ,a=2
,a=2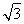 .
.
因为点(2 ,1)在椭圆
,1)在椭圆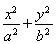 =1上,所以
=1上,所以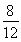 +
+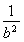 =1,解得b=
=1,解得b=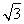 .
.
所以所求椭圆的方程为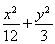 =1.
=1.
(2)设A(x1,y1),B(x2,y2)(y1<0,y2>0).点F的坐标为F(3,0).
则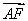 =3
=3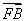 .,得
.,得 即
即 ①
①
又点A,B在椭圆C上,所以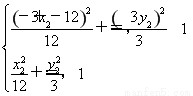 解得
解得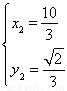 ?
?
所以B 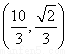 ,代入①,得点A的坐标为(2,-
,代入①,得点A的坐标为(2,-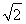 ).
).
因为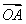 ·
·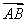 =0,所以OA⊥AB.
=0,所以OA⊥AB.
所以过O,A,B三点的圆就是以OB为直径的圆.
其方程为x2+y2-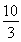 x-
x-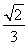 y=0.
y=0.

练习册系列答案
相关题目