题目内容
已知函数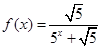 ,
,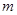 为正整数.
为正整数.
(Ⅰ)求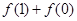 和
和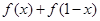 的值;
的值;
(Ⅱ)数列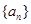 的通项公式为
的通项公式为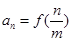 (
(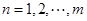 ),求数列
),求数列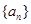 的前
的前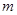 项和
项和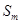 ;
;
(Ⅲ)设数列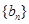 满足:
满足: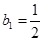 ,
,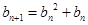 ,设
,设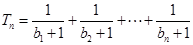 ,若(Ⅱ)中的
,若(Ⅱ)中的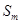 满足:对任意不小于3的正整数n,
满足:对任意不小于3的正整数n,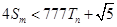 恒成立,试求m的最大值.
恒成立,试求m的最大值.
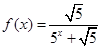 ,
,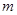 为正整数.
为正整数.(Ⅰ)求
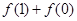 和
和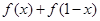 的值;
的值;(Ⅱ)数列
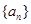 的通项公式为
的通项公式为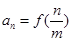 (
(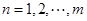 ),求数列
),求数列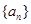 的前
的前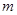 项和
项和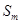 ;
;(Ⅲ)设数列
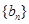 满足:
满足: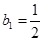 ,
,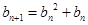 ,设
,设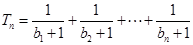 ,若(Ⅱ)中的
,若(Ⅱ)中的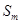 满足:对任意不小于3的正整数n,
满足:对任意不小于3的正整数n,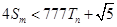 恒成立,试求m的最大值.
恒成立,试求m的最大值.(Ⅰ)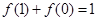
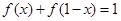 (Ⅱ)
(Ⅱ) 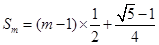
(Ⅲ) 650
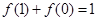
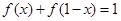 (Ⅱ)
(Ⅱ) 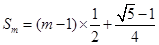
(Ⅲ) 650
试题分析:(Ⅰ)
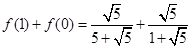 =1; 2分
=1; 2分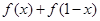 =
=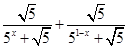 =
=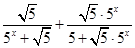 =1; 4分
=1; 4分(Ⅱ)由(Ⅰ)得
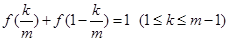 ,
,即
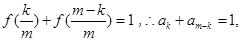
由
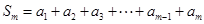 , ①
, ① 得
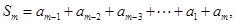 ②
② 由①+②, 得
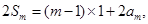
∴
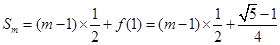 , 10分
, 10分(Ⅲ) 解:∵
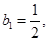
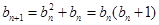 ,∴对任意的
,∴对任意的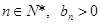 .
. ∴
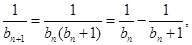 即
即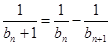 .
. ∴
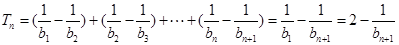 .
. ∵
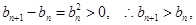 ∴数列
∴数列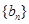 是单调递增数列.
是单调递增数列. ∴
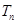 关于n递增. 当
关于n递增. 当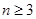 , 且
, 且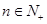 时,
时, 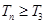 .
. ∵
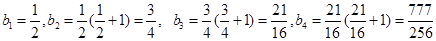
∴
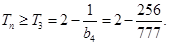
∴
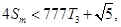
∴
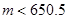 .而
.而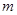 为正整数,
为正整数, ∴
 的最大值为650 16分
的最大值为650 16分点评:本题主要考查的是数列求和,其中用到了倒序相加,裂项相消等常用到的求和方法,倒序相加适用于第n项与倒数第n项之和为定值的数列,列项相消一般适用于通项公式为
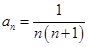 的形式的数列
的形式的数列
练习册系列答案
相关题目
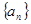 的前
的前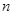 项和为
项和为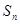 ,若
,若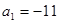 ,
,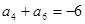 ,则当
,则当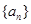 中,
中,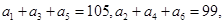 以
以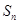 表示数列
表示数列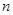 项和,则使
项和,则使



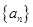 的前
的前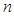 项和为
项和为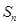 ,且
,且
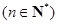 .
.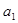 的值及数列
的值及数列
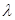 ,使不等式
,使不等式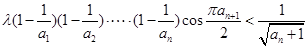
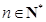 都成立?若存在,求出
都成立?若存在,求出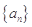 中,
中,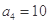 且
且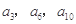 成等比数列,
成等比数列,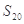 。
。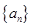 的通项
的通项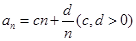 ,第2项是最小项,则
,第2项是最小项,则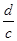 的取值范围是 .
的取值范围是 .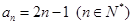 ,把数列
,把数列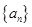 的各项排成如图所示的三角形数阵.记
的各项排成如图所示的三角形数阵.记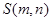 为该数阵的第
为该数阵的第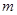 行中从左往右的第
行中从左往右的第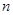 个数,则
个数,则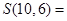 _______.
_______.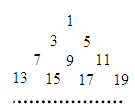
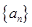 的公比
的公比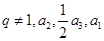 成等差数列,则
成等差数列,则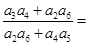 ( )
( )