题目内容
在等差数列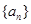 中,
中,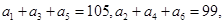 以
以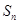 表示数列
表示数列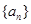 的前
的前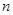 项和,则使
项和,则使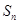 达到最大值的
达到最大值的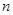 是( )
是( )
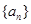 中,
中,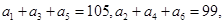 以
以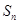 表示数列
表示数列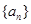 的前
的前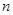 项和,则使
项和,则使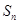 达到最大值的
达到最大值的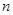 是( )
是( )A. | B. | C. | D. |
C
试题分析:因为,在等差数列
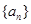 中,
中,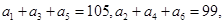 所以,由等差数列的性质,得,
所以,由等差数列的性质,得, 公差d=-2,
公差d=-2, ,因此,
,因此,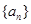 是递减数列,前20项为正数,从第21项起,所有项均为负数,故使
是递减数列,前20项为正数,从第21项起,所有项均为负数,故使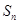 达到最大值的
达到最大值的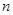 是20,选C。
是20,选C。点评:中档题,在等差数列中,m+n=p+q,
 。
。
练习册系列答案
相关题目
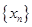 和函数
和函数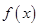 ,若
,若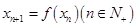 ,则称
,则称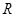 上的函数
上的函数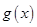 满足:对任意
满足:对任意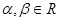 ,都有
,都有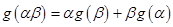 ,且
,且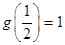 ;又数列
;又数列 满足:
满足: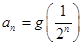 .
. 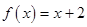 是数列
是数列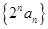 的母函数;
的母函数;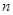 和
和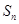 .
.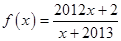 是数列
是数列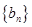 的母函数,且
的母函数,且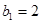 .若数列
.若数列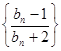 的前
的前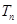 ,求证:
,求证: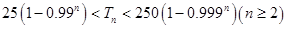 .
.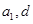 为实数,首项为
为实数,首项为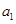 ,公差为
,公差为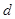 的等差数列
的等差数列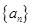 的前
的前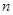 项和为
项和为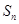 ,
,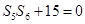 ,则
,则 的前n项和为
的前n项和为 ,若
,若 ,则
,则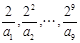 中最大的是
中最大的是 
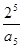
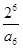

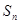
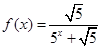 ,
,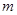 为正整数.
为正整数.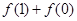 和
和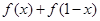 的值;
的值;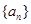 的通项公式为
的通项公式为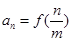 (
(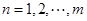 ),求数列
),求数列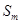 ;
;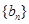 满足:
满足: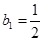 ,
,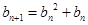 ,设
,设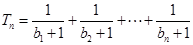 ,若(Ⅱ)中的
,若(Ⅱ)中的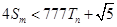 恒成立,试求m的最大值.
恒成立,试求m的最大值.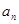 }满足
}满足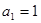 ,且
,且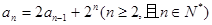
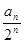 }是等差数列;
}是等差数列;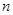 项之和
项之和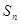 ,求证:
,求证: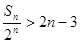 .
. 前
前 项和
项和 ,
, ,则公差d的值为 ( )
,则公差d的值为 ( )