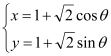题目内容
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)首先将函数![]() 的解析式写成分段函数形式,然后分段解出不等式的解集,再求它们的并集即可;(2)分
的解析式写成分段函数形式,然后分段解出不等式的解集,再求它们的并集即可;(2)分![]() 、
、![]() 、
、![]() ,然后利用三角绝对值不等式的性质求解即可.
,然后利用三角绝对值不等式的性质求解即可.
试题解析:(1)f(x)=2|x-1|+|x-2|=
所以,f(x)在(-∞,1]上递减,在[1,+∞)上递增,
又f(0)=f()=4,故f(x)≤4的解集为{x|0≤x≤}. …4分
(2)①若a>1,f(x)=(a-1)|x-1|+|x-1|+|x-a|≥a-1,
当且仅当x=1时,取等号,故只需a-1≥1,得a≥2. …6分
②若a=1,f(x)=2|x-1|,f(1)=0<1,不合题意. …7分
③若0<a<1,f(x)=a|x-1|+a|x-a|+(1-a)|x-a|≥a(1-a),
当且仅当x=a时,取等号,故只需a(1-a)≥1,这与0<a<1矛盾. …9分
综上所述,a的取值范围是[2,+∞). …10分
解法2
f(x)≥1f(1)=|1-a|≥1且a>0,解得a≥2. …6分
当a≥2时,f(x)=a|x-1|+|x-a|=
所以,f(x)在(-∞,1]上递减,在[1,+∞)上递增,则f(x)≥f(1). …8分
f(x)≥1f(1)=a-1≥1,解得a≥2.
综上所述,a的取值范围是[2,+∞). …10分

【题目】重庆市某厂党支部10月份开展“两学一做”活动,将10名党员技工平均分为甲,乙两组进行技能比赛.要求在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此分析两组技工的技术水平;
(2)质检部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,求该车间“质量合格”的概率.
【题目】某汽车公司为确定下一年度投入某种产品的宣传费,需了解年宣传费(单位:千元)对年利润![]() (单位:万元)的影响,对近5年的宣传费
(单位:万元)的影响,对近5年的宣传费![]() 和年利润
和年利润![]() (
(![]() )进行了统计,列出了下表:
)进行了统计,列出了下表:
| 2 | 4 | 7 | 17 | 30 |
| 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案.
(1)小王准备用线性回归模型拟合![]() 与
与![]() 的关系,请你帮助建立
的关系,请你帮助建立![]() 关于
关于![]() 的线性回归方程;(系数精确到0.01)
的线性回归方程;(系数精确到0.01)
(2)小李决定选择对数回归模型拟合![]() 与
与![]() 的关系,得到了回归方程:
的关系,得到了回归方程: ![]() ,并提供了相关指数
,并提供了相关指数![]() .请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据
.请用相关指数说明哪个模型更合适,并预测年宣传费为4万元的年利润.(精确到0.01)(小王也提供了他的分析数据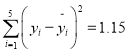 )
)
参考公式:相关指数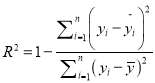
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: 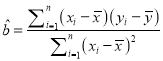 ,
, ![]() .参考数据:
.参考数据: ![]() ,
, ![]() .
.