题目内容
6.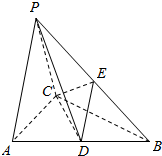 三棱锥P-ABC中△PAC是边长为4的等边三角形,△ABC为等腰直角三角形,∠ACB=90°,平面PAC⊥面 ABC,D、E分别为AB、PB的中点.
三棱锥P-ABC中△PAC是边长为4的等边三角形,△ABC为等腰直角三角形,∠ACB=90°,平面PAC⊥面 ABC,D、E分别为AB、PB的中点.(1)求证AC⊥PD;
(2)求三棱锥P-CDE的体积.
(3)(理)求点P到面CDE的距离.
分析 (1)取AC中点O,连PO,则PO⊥AC,证明AC⊥面POD,然后说明AC⊥PD.
(2)通过VP-CDE=VD-PCE,求出${S_{△PCE}}=\frac{1}{2}{S_{△PBC}}$,利用$\frac{{{V_{P-CDE}}}}{{{V_{P-ABC}}}}=\frac{1}{4}$.求解几何体的体积即可.
(3)证明BC⊥面PAC,求出CE,CD,通过几何体的体积求解点P到面CDE的距离.
解答  (1)证明:取AC中点O,连PO,则PO⊥AC,又面PAC⊥面ABC,
(1)证明:取AC中点O,连PO,则PO⊥AC,又面PAC⊥面ABC,
∴PO⊥面ABC,连OD,则OD∥BC,则DO⊥AC,
∴AC⊥面POD,∴AC⊥PD. (6分)
(2)解:VP-CDE=VD-PCE,∵E为PB中点,∴${S_{△PCE}}=\frac{1}{2}{S_{△PBC}}$,${V_{D-PCE}}=\frac{1}{2}{V_{D-PBC}}=\frac{1}{2}{V_{P-DBC}}=\frac{1}{4}{V_{P-ABC}}$,即$\frac{{{V_{P-CDE}}}}{{{V_{P-ABC}}}}=\frac{1}{4}$.
易求得${V_{P-ABC}}=\frac{{16\sqrt{3}}}{3}$,故${V_{P-CDE}}=\frac{{4\sqrt{3}}}{3}$.(8分)
(3)解:(理)∵面PAC⊥面ABC,且AC⊥BC,
∴BC⊥面PAC,∴BC⊥PC,又E为PB中点,
∴$CE=\frac{1}{2}PB=\frac{1}{2}\sqrt{P{B^2}+B{C^2}}=2\sqrt{2}$,同理得$CD=2\sqrt{2}$,
又$DE=\frac{1}{2}PA=2$,∴${S_{△CDE}}=\sqrt{7}$
∵${V_{P-CDE}}=\frac{1}{3}{S_{△CDE}}•h$,∴$h=\frac{{4\sqrt{21}}}{7}$
所以,点P到面CDE的距离为$\frac{{4\sqrt{21}}}{7}$(13分)
点评 本题考查直线与平面垂直,几何体的体积的求法,点到平面的距离的求法,考查计算能力.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案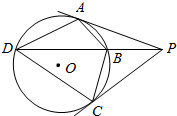 如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证:
如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证: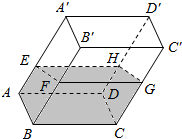 如图,在透明塑料制成的长方体ABCD-A′B′C′D′容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
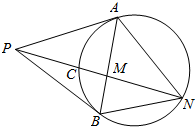
如图,在透明塑料制成的长方体ABCD-A′B′C′D′容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法: 如图,⊙O的半径OC垂直于直径AB,M为OB上一点,CM的延长线交⊙O于N,过N点的切线交AB的延长线于P.
如图,⊙O的半径OC垂直于直径AB,M为OB上一点,CM的延长线交⊙O于N,过N点的切线交AB的延长线于P. 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.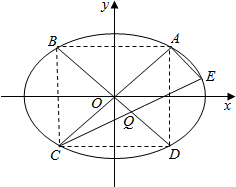 设A(x0,y0)(x0,y0≠0)是椭圆T:$\frac{{x}^{2}}{m+1}$+y2=1(m>0)上一点,它关于y轴、原点、x轴的对称点依次为B,C,D.E是椭圆T上不同于A的另外一点,且AE⊥AC,如图所示.
设A(x0,y0)(x0,y0≠0)是椭圆T:$\frac{{x}^{2}}{m+1}$+y2=1(m>0)上一点,它关于y轴、原点、x轴的对称点依次为B,C,D.E是椭圆T上不同于A的另外一点,且AE⊥AC,如图所示. 如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰好是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.
如图,正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形,P是EF与GH的交点,若矩形PFCH的面积恰好是矩形AGPE面积的2倍,试确定∠HAF的大小,并证明你的结论.