Question

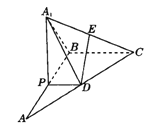
【题目】如图，在△ABC中，∠B＝90°，AB＝BC＝2，P为AB边上一动点，PD∥BC交AC于点D，现将△PDA沿PD翻折至△PDA1，E是A1C的中点．

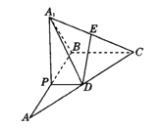
（1）若P为AB的中点，证明：DE∥平面PBA1．

（2）若平面PDA1⊥平面PDA，且DE⊥平面CBA1，求四棱锥A1﹣PBCD的体积．

Answer 1

【答案】（1）详见解析（2）

【解析】

（1）根据线面平行的判定定理可知，需证明线线平行，取的中点，连接，可证明四边形是平行四边形，可证明，（2）根据面面垂直，可证明平面，那么.

（1）证明：令的中点为，连接，.因为为的中点且,

所以是的中位线，所以,.

因为是的中点,且F为的中点,所以是的中位线,所以，且，于是有,

所以四边形为平行四边形,所以,

又平面，平面

所以有平面.

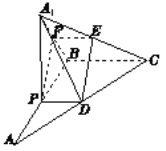
（2）解：因为平面，所以.

又因为是的中点，所以，

即是的中点.由可得，是的中点.

因为在中,，，沿翻折至，且平面平面，

利用面面垂直的性质可得平面，

所以.