题目内容
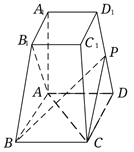
【题目】如图,在四棱锥![]() 中,
中,![]() 是等腰三角形,且
是等腰三角形,且![]() .四边形
.四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)当平面![]()
![]() 平面
平面![]() 时,求四棱锥
时,求四棱锥![]() 的体积;
的体积;
(Ⅲ)请在图中所给的五个点![]() 中找出两个点,使得这两点所在的直线与直线
中找出两个点,使得这两点所在的直线与直线![]() 垂直,并给出证明.
垂直,并给出证明.
【答案】(1)见解析; (2)![]() ; (3)见解析.
; (3)见解析.
【解析】
(Ⅰ)由已知AB∥DC,直接利用线面平行的判定证明AB∥平面PDC;(Ⅱ)取BC中点D,由
PB=PC,可得PD⊥BC,结合面面垂直的性质可得PD⊥平面ABCD,则PD为四棱锥P﹣ABCD的
高,求出底面直角梯形的面积,代入棱锥体积公式求四棱锥P﹣ABCD的体积;(Ⅲ)图中PA
⊥BC.由(Ⅱ)知,PD⊥BC,作CG⊥AB,在直角三角形CGB中,可得cos![]() ,再求
,再求
解三角形可得AD⊥BC,由线面垂直的判定可得BC⊥平面PAD,从而得到PA⊥BC.
(Ⅰ)证明:∵AB∥DC,且DC平面PDC,AB平面PDC,
∴AB∥平面PDC;
(Ⅱ)解:取BC中点D,∵PB=PC,∴PD⊥BC,
又平面PBC⊥平面ABCD,且平面PBC∩平面ABCD=BC,
∴PD⊥平面ABCD,则PD为四棱锥P﹣ABCD的高,
在底面直角梯形ABCD中,由AB=5,AD=4,DC=3,
得![]() ,且BC=
,且BC=![]() .
.
又PB=PC=3,∴PD=![]() .
.
∴![]() ;
;
(Ⅲ)解:图中PA⊥BC.
证明如下:由(Ⅱ)知,PD⊥BC,
作CG⊥AB,在直角三角形CGB中,可得cos![]() ,
,
在三角形ADB中,由余弦定理可得![]() ,
,
则AD2+BD2=AB2,
∴AD⊥BC,
又AD∩PD=D,∴BC⊥平面PAD,则PA⊥BC.

练习册系列答案
相关题目