题目内容
【题目】如图,ABC﹣A1B1C1是底面边长为2,高为 ![]() 的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).、
的正三棱柱,经过AB的截面与上底面相交于PQ,设C1P=λC1A1(0<λ<1).、 
(1)证明:PQ∥A1B1;
(2)当 ![]() 时,求点C到平面APQB的距离.
时,求点C到平面APQB的距离.
【答案】
(1)证明:∵平面ABC∥平面A1B1C1,平面ABC∩平面ABQP=AB,平面ABQP∩平面A1B1C1=QP,
∴AB∥PQ,
又∵AB∥A1B1,
∴PQ∥A1B1.
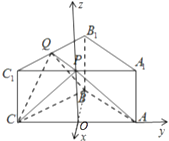
(2)解:建立如图所示的直角坐标系.
∴O(0,0,0),P(0,0, ![]() ),A(0,1,0),B(﹣
),A(0,1,0),B(﹣ ![]() ,0,0),C(0,﹣1,0),
,0,0),C(0,﹣1,0),
∴ ![]() =(0,﹣1,
=(0,﹣1, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,﹣1,0),
,﹣1,0), ![]() =(0,﹣2,0),
=(0,﹣2,0),
设平面APQB的法向量为 ![]() =(x,y,z),
=(x,y,z),
则  ,可得
,可得 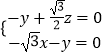 ,
,
取 ![]() =
= ![]() ,
,
∴点C到平面APQB的距离d= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由平面ABC∥平面A1B1C1 , 利用线面平行的性质定理可得:AB∥PQ,又AB∥A1B1 , 即可证明PQ∥A1B1 . (2)建立如图所示的直角坐标系.设平面APQB的法向量为 ![]() =(x,y,z),则
=(x,y,z),则  ,利用点C到平面APQB的距离d=
,利用点C到平面APQB的距离d= ![]() 即可得出.
即可得出.
【考点精析】解答此题的关键在于理解棱柱的结构特征的相关知识,掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目