Question

一个与球心距离为1的平面截球体所得的圆面面积为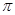，则球的体积为

A．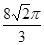

B．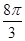

C．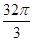

D．8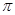

Answer 1

A

解析考点：球的体积和表面积．
分析：求出小圆的半径，利用球心到该截面的距离为1 cm，小圆的半径，通过勾股定理求出球的半径，即可求出球的体积．
解答：解：用一平面去截球所得截面的面积为π，所以小圆的半径为1
已知球心到该截面的距离为1，所以球的半径为r==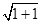
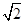
所以球的体积为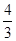：πr³=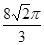
故答案为：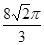
点评：本题考查球的小圆的半径，球心到该截面的距离，球的半径之间的关系，考查计算能力，是基础题．