Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ’ż∑ĹŐŚ![]() ÷–£¨
÷–£¨ ![]() ∑÷Īū «ņ‚
∑÷Īū «ņ‚![]() Ķń÷–Ķ„£¨
Ķń÷–Ķ„£¨ ![]() ő™ņ‚
ő™ņ‚![]() …Ō“ĽĶ„£¨«““ž√ś÷ĪŌŖ
…Ō“ĽĶ„£¨«““ž√ś÷ĪŌŖ![]() ”Ž
”Ž![]() ňý≥…Ĺ«Ķń”ŗŌ“÷Ķő™
ňý≥…Ĺ«Ķń”ŗŌ“÷Ķő™![]() .
.
£®1£©÷§√ų£ļ ![]() ő™
ő™![]() Ķń÷–Ķ„£Ľ
Ķń÷–Ķ„£Ľ
£®2£©«ů∆Ĺ√ś![]() ”Ž∆Ĺ√ś
”Ž∆Ĺ√ś![]() ňý≥…»Ů∂Ģ√śĹ«Ķń”ŗŌ“÷Ķ.
ňý≥…»Ů∂Ģ√śĹ«Ķń”ŗŌ“÷Ķ.
°ĺīūįł°Ņ£®1£©ľŻĹ‚őŲ£®2£©![]()
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ£®1£©“‘![]() ő™◊ÝĪÍ‘≠Ķ„£¨Ĺ®ŃĘ»ÁÕľňý ĺĶńŅ’ľš÷ĪĹ«◊ÝĪÍŌĶ
ő™◊ÝĪÍ‘≠Ķ„£¨Ĺ®ŃĘ»ÁÕľňý ĺĶńŅ’ľš÷ĪĹ«◊ÝĪÍŌĶ![]() £¨≤Ľ∑ŃŃÓ’ż∑ĹŐŚĶńņ‚≥§ő™2£¨…Ť
£¨≤Ľ∑ŃŃÓ’ż∑ĹŐŚĶńņ‚≥§ő™2£¨…Ť![]() £¨ņŻ”√
£¨ņŻ”√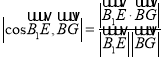 £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]() £¨ľīŅ…÷§Ķ√£Ľ
£¨ľīŅ…÷§Ķ√£Ľ
£®2£©∑÷Īū«ůĶ√∆Ĺ√ś![]() ”Ž∆Ĺ√ś
”Ž∆Ĺ√ś![]() Ķń∑®ŌÚŃŅ
Ķń∑®ŌÚŃŅ![]() £¨ņŻ”√
£¨ņŻ”√![]() «ůĹ‚ľīŅ….
«ůĹ‚ľīŅ….
‘Ő‚Ĺ‚őŲ£ļ
£®1£©÷§√ų£ļ“‘![]() ő™◊ÝĪÍ‘≠Ķ„£¨Ĺ®ŃĘ»ÁÕľňý ĺĶńŅ’ľš÷ĪĹ«◊ÝĪÍŌĶ
ő™◊ÝĪÍ‘≠Ķ„£¨Ĺ®ŃĘ»ÁÕľňý ĺĶńŅ’ľš÷ĪĹ«◊ÝĪÍŌĶ![]() .
.
≤Ľ∑ŃŃÓ’ż∑ĹŐŚĶńņ‚≥§ő™2£¨
‘Ú![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨ ![]() £¨
£¨
…Ť![]() £¨‘Ú
£¨‘Ú![]() £¨
£¨ ![]() £¨
£¨
ňý“‘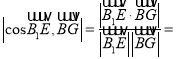
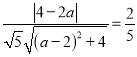 £¨
£¨
ňý“‘![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]() £®
£®![]() …Š»•£©£¨ľī
…Š»•£©£¨ľī![]() ő™
ő™![]() Ķń÷–Ķ„.
Ķń÷–Ķ„.
£®2£©Ĺ‚£ļ”…£®1£©Ņ…Ķ√![]() £¨
£¨ ![]() £¨
£¨
…Ť![]() «∆Ĺ√ś
«∆Ĺ√ś![]() Ķń∑®ŌÚŃŅ£¨
Ķń∑®ŌÚŃŅ£¨
‘Ú![]() .ŃÓ
.ŃÓ![]() £¨Ķ√
£¨Ķ√![]() .
.
“◊Ķ√∆Ĺ√ś![]() Ķń“ĽłŲ∑®ŌÚŃŅő™
Ķń“ĽłŲ∑®ŌÚŃŅő™![]() £¨
£¨
ňý“‘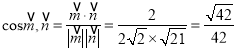 .
.
ňý“‘ňý«ů»Ů∂Ģ√śĹ«Ķń”ŗŌ“÷Ķő™![]() .
.
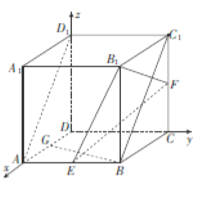
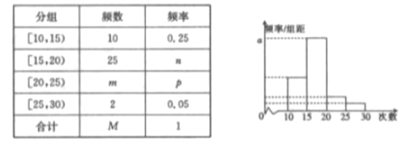
Ķ„ĺ¶£ļŅ’ľšŌÚŃŅĹ‚īūŃĘŐŚľłļőő Ő‚Ķń“Ľį„≤Ĺ÷Ť «£ļ£®1£©ĻŘ≤žÕľ–ő£¨Ĺ®ŃĘ«°ĶĪĶńŅ’ľš÷ĪĹ«◊ÝĪÍŌĶ£Ľ£®2£©–ī≥ŲŌŗ”¶Ķ„Ķń◊ÝĪÍ£¨«ů≥ŲŌŗ”¶÷ĪŌŖĶń∑ĹŌÚŌÚŃŅ£Ľ£®3£©…Ť≥ŲŌŗ”¶∆Ĺ√śĶń∑®ŌÚŃŅ£¨ņŻ”√ŃĹ÷ĪŌŖīĻ÷Ī żŃŅĽżő™Ń„Ń–≥Ų∑Ĺ≥Ő◊ť«ů≥Ų∑®ŌÚŃŅ£Ľ£®4£©ĹęŅ’ľšőĽ÷√ĻōŌĶ◊™ĽĮő™ŌÚŃŅĻōŌĶ£Ľ£®5£©łýĺ›∂®ņŪĹŠ¬Ř«ů≥ŲŌŗ”¶ĶńĹ«ļÕĺŗņŽ.
°ĺŐ‚–Õ°ŅĹ‚īūŐ‚
°ĺĹŠ Ý°Ņ
22
°ĺŐ‚ńŅ°Ņ“—÷™Õ÷‘≤![]() Ķń∂Ő÷Š≥§ő™2£¨«“Õ÷‘≤
Ķń∂Ő÷Š≥§ő™2£¨«“Õ÷‘≤![]() ĻżĶ„
ĻżĶ„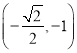 .
.
£®1£©«ůÕ÷‘≤![]() Ķń∑Ĺ≥Ő£Ľ
Ķń∑Ĺ≥Ő£Ľ
£®2£©…Ť÷ĪŌŖ![]() Ļż∂®Ķ„
Ļż∂®Ķ„![]() £¨«“–Ī¬ ő™
£¨«“–Ī¬ ő™![]() £¨»ŰÕ÷‘≤
£¨»ŰÕ÷‘≤![]() …Ōīś‘ŕ
…Ōīś‘ŕ![]() ŃĹĶ„Ļō”ŕ÷ĪŌŖ
ŃĹĶ„Ļō”ŕ÷ĪŌŖ![]() ∂‘≥∆£¨
∂‘≥∆£¨ ![]() ő™◊ÝĪÍ‘≠Ķ„£¨«ů
ő™◊ÝĪÍ‘≠Ķ„£¨«ů![]() Ķń»°÷Ķ∑∂őßľį
Ķń»°÷Ķ∑∂őßľį![]() √śĽżĶń◊Óīů÷Ķ.
√śĽżĶń◊Óīů÷Ķ.
°ĺīūįł°Ņ£®1£©![]() £®2£©
£®2£©![]()
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ£®1£©Õ÷‘≤![]() Ķń∂Ő÷Š≥§ő™
Ķń∂Ő÷Š≥§ő™![]() £¨Ķ√
£¨Ķ√![]() £¨‘Ŕ”…Õ÷‘≤…Ō“ĽĶ„Ń–∑Ĺ≥Ő«ůĹ‚
£¨‘Ŕ”…Õ÷‘≤…Ō“ĽĶ„Ń–∑Ĺ≥Ő«ůĹ‚![]() ľīŅ…£Ľ
ľīŅ…£Ľ
£®2£©…Ť÷ĪŌŖ![]() Ķń∑Ĺ≥Őő™
Ķń∑Ĺ≥Őő™![]() £¨”ŽÕ÷‘≤Ń™ŃĘĶ√
£¨”ŽÕ÷‘≤Ń™ŃĘĶ√![]() £¨ņŻ”√ő§īÔ∂®ņŪ«ůĶ√ŌŖ∂ő
£¨ņŻ”√ő§īÔ∂®ņŪ«ůĶ√ŌŖ∂ő![]() Ķń÷–Ķ„ő™
Ķń÷–Ķ„ő™![]() £¨īķ»Ž÷ĪŌŖ
£¨īķ»Ž÷ĪŌŖ![]() Ņ…Ķ√£¨
Ņ…Ķ√£¨ ![]() £¨ĹŠļŌ
£¨ĹŠļŌ![]() ľīŅ…«ůĶ√
ľīŅ…«ůĶ√![]() Ķń»°÷Ķ∑∂őߣ¨‘Ŕ«ů
Ķń»°÷Ķ∑∂őߣ¨‘Ŕ«ů![]() ļÕ‘≠Ķ„
ļÕ‘≠Ķ„![]() ĶĹ÷ĪŌŖ
ĶĹ÷ĪŌŖ![]() ĶńĺŗņŽ
ĶńĺŗņŽ![]() £¨Õ®Ļż
£¨Õ®Ļż![]() £¨ņŻ”√ő§īÔ∂®ņŪīķ»Ž«ů◊Ó÷ĶľīŅ….
£¨ņŻ”√ő§īÔ∂®ņŪīķ»Ž«ů◊Ó÷ĶľīŅ….
‘Ő‚Ĺ‚őŲ£ļ
£®1£©°ŖÕ÷‘≤![]() Ķń∂Ő÷Š≥§ő™2£¨°ŗ
Ķń∂Ő÷Š≥§ő™2£¨°ŗ![]() £¨ľī
£¨ľī![]() .
.
”÷Ķ„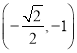 ‘ŕ
‘ŕ![]() …Ō£¨°ŗ
…Ō£¨°ŗ![]() £¨°ŗ
£¨°ŗ![]() .
.
°ŗÕ÷‘≤![]() Ķń∑Ĺ≥Őő™
Ķń∑Ĺ≥Őő™![]() .
.
£®2£©”…Ő‚“‚…Ť÷ĪŌŖ![]() Ķń∑Ĺ≥Őő™
Ķń∑Ĺ≥Őő™![]() £¨
£¨
”…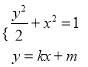 £¨ŌŻ»•
£¨ŌŻ»•![]() Ķ√£¨
Ķ√£¨ ![]() £¨
£¨
°ŗ![]() £¨ľī
£¨ľī![]() £¨ĘŔ
£¨ĘŔ
«“![]() £¨
£¨ ![]() £¨
£¨
°ŗŌŖ∂ő![]() ÷–Ķ„ĶńļŠ◊ÝĪÍ
÷–Ķ„ĶńļŠ◊ÝĪÍ![]() £¨◊›◊ÝĪÍ
£¨◊›◊ÝĪÍ![]() £¨
£¨
ľīŌŖ∂ő![]() Ķń÷–Ķ„ő™
Ķń÷–Ķ„ő™![]() .
.
Ĺę![]() īķ»Ž÷ĪŌŖ
īķ»Ž÷ĪŌŖ![]() Ņ…Ķ√£¨
Ņ…Ķ√£¨ ![]() £¨Ęŕ
£¨Ęŕ
”…ĘŔ£¨ĘŕŅ…Ķ√£¨ ![]() £¨°ŗ
£¨°ŗ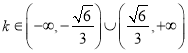 .
.
”÷![]()
 £¨
£¨
«“‘≠Ķ„![]() ĶĹ÷ĪŌŖ
ĶĹ÷ĪŌŖ![]() ĶńĺŗņŽ
ĶńĺŗņŽ £¨
£¨
°ŗ![]()
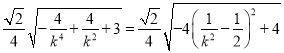 £¨
£¨
°Ŗ![]() £¨°ŗ
£¨°ŗ![]() £¨°ŗĶĪ
£¨°ŗĶĪ![]() Ī£¨
Ī£¨ ![]() »°Ķ√◊Óīů÷Ķ
»°Ķ√◊Óīů÷Ķ![]() .
.