Question

【题目】已知圆P过.

（1）求圆P的方程；

（2）若过点的直线l被圆P所截得的弦长为8，求直线l的方程.

Answer 1

【答案】（1）；（2）或.

【解析】

(1)设出圆的一般方程，将三点坐标代入得方程组，解出即可.
(2) 由半径、半弦长、弦心距构成的直角三角形可得圆心到直线的距离为3，分直线的斜率存在和不存在进行计算即可.

（1）设圆P的方程为：.

∵A，B，C都在圆上，

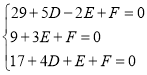∴，解得.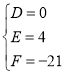

∴所求圆P的方程为.

（2）由，知圆心，半径，

由直线l被圆p截得的弦长为8，得圆心距

当直线l与x轴不垂直时，设直线l方程为：，

即，

∴圆心P到直线l距离，化简得，则.

∴直线l方程为：，即

当直线轴时，直线l方程为，

代入圆方程得，解得，

∴弦长仍为8，满足题意.

综上，直线l的方程为或