题目内容
19.化简:$\frac{si{n}^{2}α-si{n}^{2}β}{sinαcosα-sinβcosβ}$.分析 由降幂公式,倍角公式化简后,根据和差化积公式及同角三角函数关系式即可化简得解.
解答 解:$\frac{si{n}^{2}α-si{n}^{2}β}{sinαcosα-sinβcosβ}$=$\frac{\frac{1-cos2α}{2}-\frac{1-cos2β}{2}}{\frac{1}{2}sin2α-\frac{1}{2}sin2β}$=$\frac{cos2β-cos2α}{sin2α-sin2β}$=$\frac{-2sin(α+β)sin(β-α)}{2cos(α+β)sin(α-β)}$=tan(α+β).
点评 本题主要考查了降幂公式,倍角公式,和差化积公式及同角三角函数关系式的应用,属于基础题.

练习册系列答案
相关题目
7.某大学的一个社会实践调查小组,在对大学生的良好“光盘习惯”的调查中,随机发放了120份问卷,对回收的100份有效问卷进行统计,得到如下2×2列联表:
(1)现已按是否做到关盘分层从45份女生问卷中抽取了9份问卷,若从这9份问卷中随机抽取4份,并记其中能做到光盘的问卷的分数为ξ,试求随机变量ξ的分布列和数学期望;
(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过P,那么,根据临界值表,最精确的P的值应为多少?请说明理由.
| 做不到光盘 | 能做到光盘 | 合计 | |
| 男 | 45 | 10 | 55 |
| 女 | 30 | 15 | 45 |
| 合计 | 70 | 25 | 100 |
(2)如果认为良好“光盘习惯”与性别有关犯错误的概率不超过P,那么,根据临界值表,最精确的P的值应为多少?请说明理由.
8.从男生7人和女生5人中选出4人进行乒乓球混双比赛,则不同的种数为( )
| A. | 420种 | B. | 210种 | C. | 840种 | D. | 105种 |
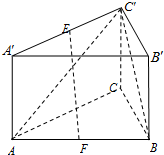 如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.
如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点. 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,过点F2的直线与椭圆C相交于A、B两点,∠F1F2B=$\frac{2π}{3}$,△F1F2A的面积是△F1F2B的面积的2倍,若|AB|=$\frac{15}{2}$,求椭圆C的方程.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,过点F2的直线与椭圆C相交于A、B两点,∠F1F2B=$\frac{2π}{3}$,△F1F2A的面积是△F1F2B的面积的2倍,若|AB|=$\frac{15}{2}$,求椭圆C的方程.