题目内容
(本小题满分13分) 设椭圆E中心在原点,焦点在x轴上,短轴长为4,点M(2, )在椭圆上,。
)在椭圆上,。
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且 ,求△OAB的面积的取值范围。
,求△OAB的面积的取值范围。
 )在椭圆上,。
)在椭圆上,。(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且
 ,求△OAB的面积的取值范围。
,求△OAB的面积的取值范围。(1) ;(2)S
;(2)S 。
。
 ;(2)S
;(2)S 。
。试题分析:(1)因为椭圆E:
 (a>b>0)过M(2,
(a>b>0)过M(2, ) ,2b=4
) ,2b=4故可求得b=2,a=2
 椭圆E的方程为
椭圆E的方程为 ……2分
……2分(2)设A(x1,y1),B(x2,y2),当直线L斜率存在时设方程为
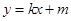 ,
,解方程组
 得
得 ,即
,即 ,
,则△=
 ,
,即
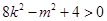 (*)……………………4分
(*)……………………4分 ,
, 要使
要使 ,需使
,需使 ,即
,即 ,
,所以
 , 即
, 即 ①………………………7分
①………………………7分将它代入(*)式可得
 ……………………………8分
……………………………8分P到L的距离为

又

将
 及韦达定理代入可得
及韦达定理代入可得 ……………………10分
……………………10分当
 时
时
由
 故
故 ……………12分
……………12分当
 时,
时, 
当AB的斜率不存在时,
 ,
,综上S
 ……………………………13分
……………………………13分点评:求椭圆的标准方程是解析几何的基本问题,涉及直线与椭圆的位置关系问题,常常运用韦达定理,本题属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
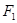
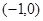 、
、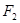
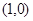 为椭圆的焦点,且直线
为椭圆的焦点,且直线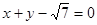 与椭圆相切.
与椭圆相切.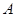 、
、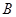 两点,求△
两点,求△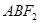 的面积
的面积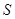 的最大值,并求此时直线的方程。
的最大值,并求此时直线的方程。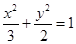 的左、右顶点分别为
的左、右顶点分别为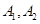 ,点M是椭圆上异于
,点M是椭圆上异于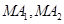 的斜率分别为
的斜率分别为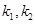 ,求证
,求证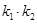 为定值并求出此定值;
为定值并求出此定值;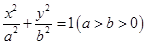 的左、右顶点分别为
的左、右顶点分别为 与椭圆
与椭圆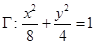 相似,且椭圆
相似,且椭圆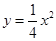 的焦点.
的焦点.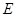 的中心在原点,对称轴在坐标轴上,直线
的中心在原点,对称轴在坐标轴上,直线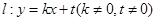 与椭圆
与椭圆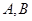 两点,且与椭圆
两点,且与椭圆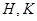 两点.若线段
两点.若线段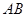 与线段
与线段 的中点重合,试判断椭圆
的中点重合,试判断椭圆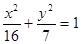 的左右焦点分别为
的左右焦点分别为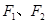 ,过焦点
,过焦点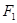 的直线交椭圆于
的直线交椭圆于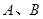 两点,若
两点,若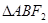 的内切圆的面积为
的内切圆的面积为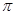 ,设
,设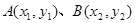 ,则
,则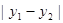 值为 .
值为 .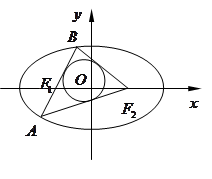
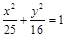 的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则
的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则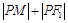 的最大值为__________.
的最大值为__________.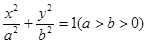 的离心率为
的离心率为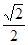 ,且过点
,且过点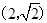 .
.
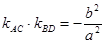 ,
,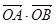 的最值.
的最值.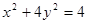 ,直线
,直线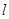 :y=x+m
:y=x+m  的值;
的值; ,若其焦点在
,若其焦点在 轴上,则
轴上,则 的取值范围是( )
的取值范围是( )


