题目内容
已知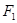
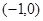 、
、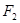
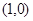 为椭圆的焦点,且直线
为椭圆的焦点,且直线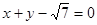 与椭圆相切.
与椭圆相切.
(Ⅰ)求椭圆方程;
(Ⅱ)过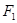 的直线交椭圆于
的直线交椭圆于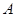 、
、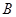 两点,求△
两点,求△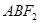 的面积
的面积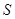 的最大值,并求此时直线的方程。
的最大值,并求此时直线的方程。
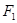
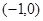 、
、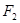
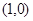 为椭圆的焦点,且直线
为椭圆的焦点,且直线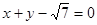 与椭圆相切.
与椭圆相切.(Ⅰ)求椭圆方程;
(Ⅱ)过
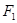 的直线交椭圆于
的直线交椭圆于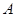 、
、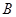 两点,求△
两点,求△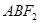 的面积
的面积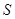 的最大值,并求此时直线的方程。
的最大值,并求此时直线的方程。(Ⅰ) ;(Ⅱ)
;(Ⅱ)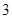 ,
,  .
.
 ;(Ⅱ)
;(Ⅱ)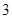 ,
,  .
.试题分析:(Ⅰ)依题意可设椭圆方程为
 ,
,由
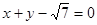 得
得 代入
代入 消去
消去 并整理得
并整理得 ,
,由

解得
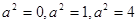 ,
,
 ,
, .
. (Ⅱ)设过
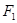 的直线:
的直线: ,代入
,代入 消去
消去 并整理得
并整理得 ,
, ,
,  ,
,当
 ,即
,即 时,面积S最大,此时直线方程为
时,面积S最大,此时直线方程为 .
.点评:求解圆锥曲线的方程关键是求解a和b,可应用已知条件得到关于两个参量的方程或由性质直接求得;求解解析几何问题也要注重对数学思想的应用,从而使问题求解方法明确、易解

练习册系列答案
相关题目
 )在椭圆上,。
)在椭圆上,。 ,求△OAB的面积的取值范围。
,求△OAB的面积的取值范围。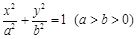 ,其离心率为
,其离心率为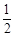 ,经过椭圆焦点且垂直于长轴的弦长为3.
,经过椭圆焦点且垂直于长轴的弦长为3.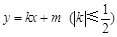 与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足
与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足 ,求
,求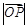 的取值范围.
的取值范围.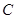 的两个焦点为
的两个焦点为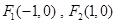 ,点
,点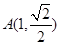 在椭圆
在椭圆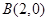 ,设点
,设点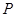 是椭圆
是椭圆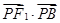 的取值范围.
的取值范围. 轴上的椭圆
轴上的椭圆 的离心率是
的离心率是 ,则
,则 的值为 ( )
的值为 ( )

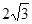

 到两定点
到两定点 、
、 的距离和为8,且
的距离和为8,且 ,线段
,线段 的的中点为
的的中点为 ,过点
,过点 条
条 条
条 条
条 条
条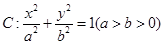 过点
过点 ,且离心率为
,且离心率为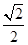 .
.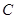 的方程;
的方程;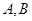 为椭圆
为椭圆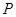 是椭圆
是椭圆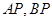 分别交直线
分别交直线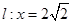 于
于 两点.
两点. 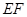 为直径的圆恒过
为直径的圆恒过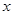 轴上的定点.
轴上的定点.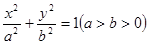 的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )
的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )


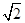 -1
-1 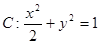 的两焦点为
的两焦点为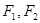 ,点
,点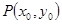 满足
满足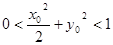 ,则
,则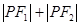 的取值范围为 ,直线
的取值范围为 ,直线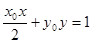 与椭圆
与椭圆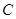 的公共点个数为 .
的公共点个数为 .