Question

【题目】已知a＞0，设命题p：函数f（x）=x2﹣2ax+1﹣2a在区间[0，1]上与x轴有两个不同的交点；命题q：g（x）=|x﹣a|﹣ax有最小值．若（￢p）∧q是真命题，求实数a的取值范围．

Answer 1

【答案】解：若p真，则 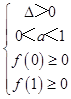，即
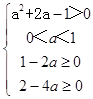
∴ ＜a≤ ．
若q真，g（x）=|x﹣a|﹣ax= ，
∵a＞0，
∴﹣（1+a）＜0，
即g（x）在（﹣∞，a）单调递减的，要使g（x）有最小值，则g（x）在[a，+∞）增或为常数，
即1﹣a≥0，
∴0＜a≤1，
若（￢p）∧q是真命题，则p为假命题且q为真命题，
∴
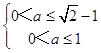
解得：a∈（0， ]∪（ ，1]
【解析】由（￢p）∧q是真命题，得：p假且q真；分别求出命题p，q为真假是参数a的范围，可得答案．
【考点精析】本题主要考查了命题的真假判断与应用的相关知识点，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系才能正确解答此题．