题目内容
12.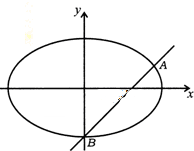 如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的下顶点为B,右焦点为F,直线BF与椭圆E的另一个交点为A,$\overrightarrow{BF}=3\overrightarrow{FA}$.
如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的下顶点为B,右焦点为F,直线BF与椭圆E的另一个交点为A,$\overrightarrow{BF}=3\overrightarrow{FA}$.(Ⅰ)求椭圆E的离心率;
(Ⅱ)若点P为椭圆上的一个动点,且△PAB面积的最大值为$\frac{{2\sqrt{3}+2}}{3}$,求椭圆E的方程.
分析 (I)由B(0,-b),F(c,0),$\overrightarrow{BF}=3\overrightarrow{FA}$.可得A$(\frac{4}{3}c,\frac{1}{3}b)$,代入椭圆的标准方程即可得出e.
(II)由(I)可知:a=$\sqrt{2}$c,b=c.可得kBF=1,$A(\frac{4}{3}c,\frac{1}{3}c)$,B(0,-c),|AB|=$\frac{4\sqrt{2}}{3}$c,直线AB的方程为:y=x-c.当△PAB面积取最大值时,动点P离直线AB的距离最大.设直线l:y=x+m(m>0),为椭圆的一条切线,与椭圆的方程联立可得3x2+4mx+2m2-2c2=0,由△=0,可得$m=\sqrt{3}$c,可得直线l与AB的距离d=$\frac{|\sqrt{3}c+c|}{\sqrt{2}}$,此时S△PAB=$\frac{1}{2}|AB|d$=$\frac{2\sqrt{3}+2}{3}$,解出即可.
解答 解:(I)∵B(0,-b),F(c,0),$\overrightarrow{BF}=3\overrightarrow{FA}$.
可得A$(\frac{4}{3}c,\frac{1}{3}b)$,
代入椭圆的标准方程可得:$\frac{(\frac{4}{3}c)^{2}}{{a}^{2}}+\frac{(\frac{b}{3})^{2}}{{b}^{2}}=1$,
化为$\frac{c}{a}=\frac{\sqrt{2}}{2}$,
∴$e=\frac{\sqrt{2}}{2}$.
(II)由(I)可知:a=$\sqrt{2}$c,b=c.
可得kBF=1,$A(\frac{4}{3}c,\frac{1}{3}c)$,B(0,-c),
|AB|=$\frac{4\sqrt{2}}{3}$c,直线AB的方程为:y=x-c.
当△PAB面积取最大值时,动点P离直线AB的距离最大.
设直线l:y=x+m(m>0),为椭圆的一条切线,且l∥AB.
联立$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{2{c}^{2}}+\frac{{y}^{2}}{{c}^{2}}=1}\end{array}\right.$,化为3x2+4mx+2m2-2c2=0,
由△=0,可得$m=\sqrt{3}$c,即l:y=x+$\sqrt{3}c$,
直线l与AB的距离d=$\frac{|\sqrt{3}c+c|}{\sqrt{2}}$,
此时S△PAB=$\frac{1}{2}|AB|d$=$\frac{1}{2}•\frac{4\sqrt{2}}{3}c×\frac{\sqrt{3}+1}{\sqrt{2}}c$=$\frac{2\sqrt{3}+2}{3}$,
解得c=1,可得a=$\sqrt{2}$,b=1.
∴椭圆的标准方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相切问题转化为△=0、平行线之间的距离、三角形的面积计算公式,考查了推理能力与计算能力,属于难题.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
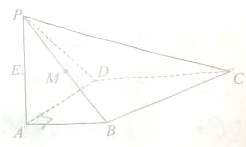 如图所示,四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点.
如图所示,四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=AB=$\frac{1}{2}$CD=1,M为PB的中点.