题目内容
7.已知$\underset{lim}{n→∞}$($\sqrt{4{n}^{2}+a}$-an)=b,求常数a、b的关系.分析 利用分子有理化、数列极限的运算法则即可得出.
解答 解:∵$\underset{lim}{n→∞}$($\sqrt{4{n}^{2}+a}$-an)=$\underset{lim}{n→∞}\frac{4{n}^{2}+a-{a}^{2}{n}^{2}}{\sqrt{4{n}^{2}+a}+an}$=$\frac{4-{a}^{2}}{2}$=b,
∴4-a2=2b.
点评 本题考查了分子有理化、数列极限的运算法则,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
17.若复数z满足|z|=1,则|z-3-4i|的最小值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
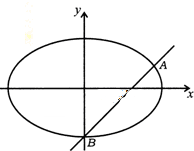 如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的下顶点为B,右焦点为F,直线BF与椭圆E的另一个交点为A,$\overrightarrow{BF}=3\overrightarrow{FA}$.
如图,已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的下顶点为B,右焦点为F,直线BF与椭圆E的另一个交点为A,$\overrightarrow{BF}=3\overrightarrow{FA}$.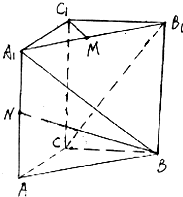 如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=2,AB=2$\sqrt{2}$,棱AA1=4,M,N分别是A1B1,AA1的中点.
如图,直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=2,AB=2$\sqrt{2}$,棱AA1=4,M,N分别是A1B1,AA1的中点.