题目内容
设点P在曲线y=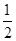 ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).
ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).
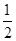 ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).
ex上,点Q在曲线y=ln(2x)上,则|PQ|的最小值为( ).| A.1-ln 2 | B.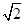 (1-ln 2) (1-ln 2) | C.1+ln 2 | D.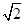 (1+ln 2) (1+ln 2) |
B
由题意知函数y=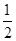 ex与y=ln(2x)互为反函数,其图象关于直线y=x对称,两曲线上点之间的最小距离就是y=x与y=
ex与y=ln(2x)互为反函数,其图象关于直线y=x对称,两曲线上点之间的最小距离就是y=x与y=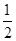 ex上点的最小距离的2倍.设y=
ex上点的最小距离的2倍.设y=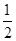 ex上点(x0,y0)处的切线与直线y=x平行.则
ex上点(x0,y0)处的切线与直线y=x平行.则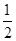 ex0=1,∴x0=ln 2,y0=1,
ex0=1,∴x0=ln 2,y0=1,
∴点(x0,y0)到y=x的距离为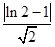 =
=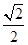 (1-ln 2),
(1-ln 2),
则|PQ|的最小值为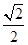 (1-ln 2)×2=
(1-ln 2)×2=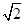 (1-ln 2).
(1-ln 2).
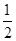 ex与y=ln(2x)互为反函数,其图象关于直线y=x对称,两曲线上点之间的最小距离就是y=x与y=
ex与y=ln(2x)互为反函数,其图象关于直线y=x对称,两曲线上点之间的最小距离就是y=x与y=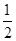 ex上点的最小距离的2倍.设y=
ex上点的最小距离的2倍.设y=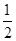 ex上点(x0,y0)处的切线与直线y=x平行.则
ex上点(x0,y0)处的切线与直线y=x平行.则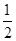 ex0=1,∴x0=ln 2,y0=1,
ex0=1,∴x0=ln 2,y0=1,∴点(x0,y0)到y=x的距离为
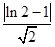 =
=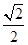 (1-ln 2),
(1-ln 2),则|PQ|的最小值为
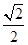 (1-ln 2)×2=
(1-ln 2)×2=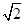 (1-ln 2).
(1-ln 2).
练习册系列答案
相关题目
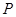 和
和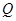 (万元),它们与投入资金
(万元),它们与投入资金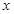 (万元)的关系依次是:其中
(万元)的关系依次是:其中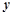 (件)与销售单价
(件)与销售单价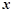 (元/件)可近似看作一次函数
(元/件)可近似看作一次函数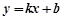 的关系(如图所示).
的关系(如图所示). 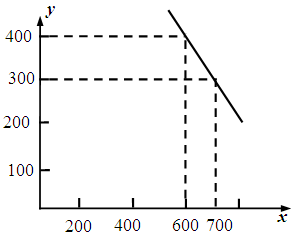
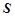 元. 试用销售单价
元. 试用销售单价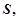 并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?
并求销售单价定为多少时,该公司获得最大毛利润?最大毛利润是多少?此时的销售量是多少?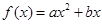
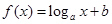

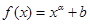
 ,对任意x∈[1,+∞),f(2mx)+2mf(x)<0恒成立,则实数m的取值范围是________.
,对任意x∈[1,+∞),f(2mx)+2mf(x)<0恒成立,则实数m的取值范围是________.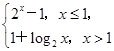 则函数f(x)的零点为________.
则函数f(x)的零点为________. (A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是 ( ).
(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是 ( ). 及点
及点 ,在
,在 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 .设
.设 所表示图形的面积为________.
所表示图形的面积为________.