题目内容
设过点P(x,y)的直线分别与x轴和y轴交于A,B两点,点Q与点P关于y轴对称,O为坐标原点,若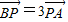 且
且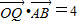 .
.(1)求点P的轨迹M的方程;
(2)过F(2,0)的直线与轨迹M交于A,B两点,求
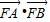 的取值范围.
的取值范围.
【答案】分析:(1)由点P(x,y),点Q与点P关于y轴对称题设知Q(-x,y),设A(a,0),B(0,b),由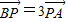 且
且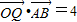 ,知
,知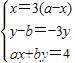 ,由此能求出点P的轨迹M的方程.
,由此能求出点P的轨迹M的方程.
(2)设过F(2,0)的直线方程为y=kx-2k,联立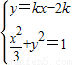 ,得(3k2+1)x2-12k2x+12k2-3=0,设A(x1,y1),B(x2,y2),由
,得(3k2+1)x2-12k2x+12k2-3=0,设A(x1,y1),B(x2,y2),由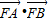 =(x1-2)(x2-2)+y1y2=(1+k2)(x1-2)(x2-2),利用韦达定理能求出
=(x1-2)(x2-2)+y1y2=(1+k2)(x1-2)(x2-2),利用韦达定理能求出 的取值范围.
的取值范围.
解答:解:(1)∵过点P(x,y)的直线分别与x轴和y轴交于A,B两点,点Q与点P关于y轴对称,
∴Q(-x,y),设A(a,0),B(0,b),
∵O为坐标原点,∴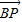 =(x,y-b),
=(x,y-b),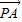 =(a-x,-y),
=(a-x,-y),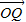 =(-x,y),
=(-x,y),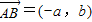 ,
,
∵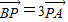 且
且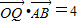 ,
,
∴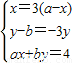 ,
,
解得点P的轨迹M的方程为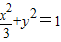 .
.
(2)设过F(2,0)的直线方程为y=kx-2k,
联立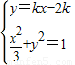 ,得(3k2+1)x2-12k2x+12k2-3=0,
,得(3k2+1)x2-12k2x+12k2-3=0,
设A(x1,y1),B(x2,y2),则x1+x2=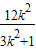 ,x1x2=
,x1x2=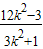 ,
,
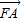 =(x1-2,y1),
=(x1-2,y1),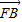 =(x2-2,y2),
=(x2-2,y2),
∴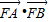 =(x1-2)(x2-2)+y1y2
=(x1-2)(x2-2)+y1y2
=(1+k2)(x1-2)(x2-2)
=(1+k2)[x1x2-2(x1+x2)+4]
=(1+k2)(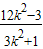 -
-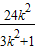 +4)
+4)
=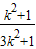
= +
+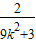 ,
,
∴当k2→∞ 的最小值→
的最小值→ ;当k=0时,
;当k=0时,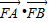 的最大值为1.
的最大值为1.
∴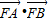 的取值范围是(
的取值范围是( ,1].
,1].
点评:本题考查椭圆方程的求法,考查向量乘积人取值范围的求法,解题时要认真审题,注意韦达定理和向量知识的合理运用.
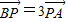 且
且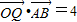 ,知
,知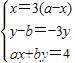 ,由此能求出点P的轨迹M的方程.
,由此能求出点P的轨迹M的方程.(2)设过F(2,0)的直线方程为y=kx-2k,联立
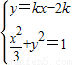 ,得(3k2+1)x2-12k2x+12k2-3=0,设A(x1,y1),B(x2,y2),由
,得(3k2+1)x2-12k2x+12k2-3=0,设A(x1,y1),B(x2,y2),由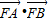 =(x1-2)(x2-2)+y1y2=(1+k2)(x1-2)(x2-2),利用韦达定理能求出
=(x1-2)(x2-2)+y1y2=(1+k2)(x1-2)(x2-2),利用韦达定理能求出 的取值范围.
的取值范围.解答:解:(1)∵过点P(x,y)的直线分别与x轴和y轴交于A,B两点,点Q与点P关于y轴对称,
∴Q(-x,y),设A(a,0),B(0,b),
∵O为坐标原点,∴
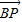 =(x,y-b),
=(x,y-b),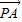 =(a-x,-y),
=(a-x,-y),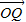 =(-x,y),
=(-x,y),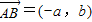 ,
,∵
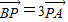 且
且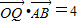 ,
,∴
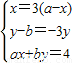 ,
,解得点P的轨迹M的方程为
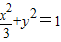 .
.(2)设过F(2,0)的直线方程为y=kx-2k,
联立
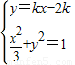 ,得(3k2+1)x2-12k2x+12k2-3=0,
,得(3k2+1)x2-12k2x+12k2-3=0,设A(x1,y1),B(x2,y2),则x1+x2=
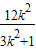 ,x1x2=
,x1x2=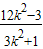 ,
,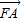 =(x1-2,y1),
=(x1-2,y1),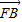 =(x2-2,y2),
=(x2-2,y2),∴
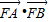 =(x1-2)(x2-2)+y1y2
=(x1-2)(x2-2)+y1y2=(1+k2)(x1-2)(x2-2)
=(1+k2)[x1x2-2(x1+x2)+4]
=(1+k2)(
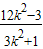 -
-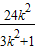 +4)
+4)=
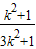
=
 +
+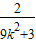 ,
,∴当k2→∞
 的最小值→
的最小值→ ;当k=0时,
;当k=0时,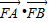 的最大值为1.
的最大值为1.∴
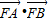 的取值范围是(
的取值范围是( ,1].
,1].点评:本题考查椭圆方程的求法,考查向量乘积人取值范围的求法,解题时要认真审题,注意韦达定理和向量知识的合理运用.

练习册系列答案
相关题目
设过点P(x,y)的直线分别与x轴的正半轴和y轴的正半轴交于A,B两点,点Q与点P关于y轴对称,O为坐标原点,若
=2
且
•
=1,则点P的轨迹方程是( )
| BP |
| PA |
| OQ |
| AB |
A、3x2+
| ||
B、3x2-
| ||
C、
| ||
D、
|
 设过点P(x,y)的直线分别与x轴的正半轴和y轴的正半轴交于A,B两点,点Q与点P关于y轴对称,O为坐标原点,若
设过点P(x,y)的直线分别与x轴的正半轴和y轴的正半轴交于A,B两点,点Q与点P关于y轴对称,O为坐标原点,若| BP |
| PA |
| 1 |
| 2 |
| OQ |
| 1 |
| 2 |
| AB |
A、x2+
| ||
B、x2-
| ||
C、
| ||
D、
|