题目内容
8.新建一个娱乐场的费用是50万元,每年的固定费用(水、电费、员工工资等)4.5万元,年维修费用第一年1万元,以后逐年递增1万元,问该娱乐乐场使用多少年时,它的平均费用最少?分析 由题意,设使用x年时平均费用最少,平均费用为y万元,所以总维修费用为$\frac{(x+1)x}{2}$元,得到解析式变形,利用基本不等式求最值.
解答 解:设使用x年时平均费用最少,平均费用为y万元,所以总维修费用为$\frac{(x+1)x}{2}$元,
则y=$\frac{50+4.5x+\frac{(1+x)x}{2}}{x}=\frac{50}{x}+\frac{x}{2}+5$≥2$\sqrt{\frac{50}{x}•\frac{x}{2}}+5$=15,
当且仅当$\frac{50}{x}=\frac{x}{2}$时,即x=10时等号成立.
所以娱乐乐场使用10年时,它的平均费用最少.
点评 本题考查了基本不等式的应用;关键是建立数学模型,根据解析式特点,利用基本不等式求最值.

练习册系列答案
相关题目
16.在正三棱锥P-ABC中,M为△ABC内(含边界)一动点,且点M到三个侧面PAB、PBC、PCA的距离成等差数列,则点M的轨迹是( )
| A. | 一条折线段 | B. | 一条线段 | C. | 一段圆弧 | D. | 一段抛物线 |
3.若0<a<1,0<b<1且a≠b,则a+b、2$\sqrt{ab}$、2ab、a2+b2中最大的一个是( )
| A. | a+b | B. | 2$\sqrt{ab}$ | C. | 2ab | D. | a2+b2 |
17.如图所示的程序运行结果为( )
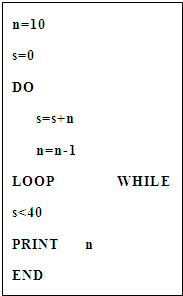
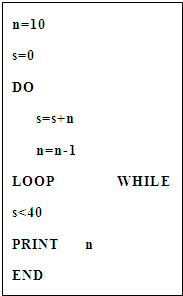
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
 一个体积为16$\sqrt{3}$的正三棱柱(即底面为正三角形,侧棱垂直底面)的三视图如图所示,则这个三棱柱的左视图的面积为8$\sqrt{3}$.
一个体积为16$\sqrt{3}$的正三棱柱(即底面为正三角形,侧棱垂直底面)的三视图如图所示,则这个三棱柱的左视图的面积为8$\sqrt{3}$.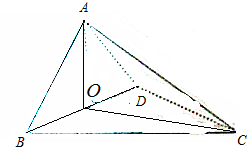 如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=$\sqrt{6}$.