题目内容
【题目】已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.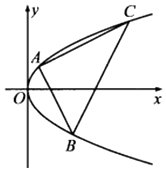
(Ⅰ)若A(1,2),B(4,﹣4),求点C的坐标;
(Ⅱ)若抛物线上存在点D,使得线段AD总被直线BC平分,求点A的坐标.
【答案】解:(Ⅰ)∵A(1,2)在抛物线y2=2px(p>0)上,∴p=2,
设C( ![]() ,t),则由AB⊥AC,得kABkAC=﹣1,
,t),则由AB⊥AC,得kABkAC=﹣1,
∵A(1,2),B(4,﹣4),kABkAC=﹣1,
∴kABkAC= ![]() ×
× ![]() =﹣1,
=﹣1,
解得t=6,即C(9,6).
(Ⅱ)设A(x0,y0),B( ![]() ),C(
),C( ![]() ),
),
则直线BC的方程为(y1+y2)(y+y0)=2p(x﹣2p﹣x0),
故直线BC恒过点E(x0+2p,﹣y0),
∴直线AE的方程为y=﹣ ![]() (x﹣x0)+y0,
(x﹣x0)+y0,
代入抛物线方程y2=2px(p>0),得点D的坐标为( ![]() ,﹣
,﹣ ![]() ),
),
∵线段AD总被直线BC平分,
∴ 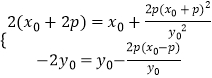 ,解得
,解得 ![]() ,
,
∴点A的坐标A( ![]() ).
).
【解析】(Ⅰ)由A(1,2)在抛物线上,求出p=2,设C( ![]() ,t),则由kABkAC=﹣1,解得t=6,由此能求出C点坐标.(Ⅱ)设A(x0,y0),B(
,t),则由kABkAC=﹣1,解得t=6,由此能求出C点坐标.(Ⅱ)设A(x0,y0),B( ![]() ),C(
),C( ![]() ),则直线BC的方程为(y1+y2)(y+y0)=2p(x﹣2p﹣x0),从而直线BC恒过点E(x0+2p,﹣y0),直线AE的方程为y=﹣
),则直线BC的方程为(y1+y2)(y+y0)=2p(x﹣2p﹣x0),从而直线BC恒过点E(x0+2p,﹣y0),直线AE的方程为y=﹣ ![]() (x﹣x0)+y0,代入抛物线方程,得D(
(x﹣x0)+y0,代入抛物线方程,得D( ![]() ,﹣
,﹣ ![]() ),利用线段AD总被直线BC平分,能求出点A的坐标.
),利用线段AD总被直线BC平分,能求出点A的坐标.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案【题目】由于雾霾日趋严重,政府号召市民乘公交出行.但公交车的数量太多会造成资源的浪费,太少又难以满足乘客需求.为此,某市公交公司在某站台的60名候车乘客中进行随机抽样,共抽取10人进行调查反馈,所选乘客情况如下表所示:
组别 | 候车时间(单位:min) | 人数 |
一 | [0,5) | 1 |
二 | [5,10) | 5 |
三 | [10,15) | 3 |
四 | [15,20) | 1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)现从这10人中随机取3人,求至少有一人来自第二组的概率;
(3)现从这10人中随机抽取3人进行问卷调查,设这3个人共来自X个组,求X的分布列及数学期望.