题目内容
【题目】已知以点![]() 为圆心的圆过原点O,与x轴另一个交点为M,与y轴另一个交点为N,
为圆心的圆过原点O,与x轴另一个交点为M,与y轴另一个交点为N,
(1)求证:△MON的面积为定值;
(2)直线4x+ y-4=0与圆C交于点A、B,若![]() ,求圆C的方程
,求圆C的方程
(3)若直线l:x+ y -5=0和圆C交于点A,B两点,且AB=![]() ,求圆心C的坐标。
,求圆心C的坐标。
【答案】(1)证明见解析;(2)![]() ;(3)(1,2)或(2,1).
;(3)(1,2)或(2,1).
【解析】
试题分析:(1)关键是求出![]() 的面积,首先写出圆
的面积,首先写出圆![]() 的方程
的方程![]() ,可化简后分别令
,可化简后分别令![]() 和
和![]() 求得
求得![]() 的坐标,从而得
的坐标,从而得![]() 的面积;(2)由
的面积;(2)由![]() ,知
,知![]() 在
在![]() 的中垂线上,从而
的中垂线上,从而![]() ,因此可得
,因此可得![]() 斜率,由此可得
斜率,由此可得![]() ,得圆
,得圆![]() 方程;(3)已知直线与圆相交弦长,可由垂径定理求得弦长,即先求得圆心
方程;(3)已知直线与圆相交弦长,可由垂径定理求得弦长,即先求得圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,由勾股定列出关于
,由勾股定列出关于![]() 的方程,解得可得圆心坐标.
的方程,解得可得圆心坐标.
试题解析:(1)由题设知,圆C的方程为![]() ,化简得
,化简得![]() ,当y=0时,x=0或2t,则
,当y=0时,x=0或2t,则![]() ;当x=0时,y=0或
;当x=0时,y=0或![]() ,则
,则![]() , ∴
, ∴![]() 为定值
为定值
(2)∵![]() ,则原点O在AB的中垂线上,设AB的中点为H,则CH⊥AB,∴C、H、O三点共线,则直线OC的斜率
,则原点O在AB的中垂线上,设AB的中点为H,则CH⊥AB,∴C、H、O三点共线,则直线OC的斜率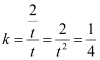 ,∴t=2
,∴t=2![]() (负舍)
(负舍)
∴圆心C(2![]() ,
, ![]() )∴圆C的方程为
)∴圆C的方程为![]()
(3)d= ,r=
,r=![]() ,弦长为
,弦长为![]() ,列出方程:
,列出方程:
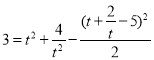 ,令
,令![]() ,方程可化为
,方程可化为![]() ,解得
,解得
m=3或-13(舍),则t=1或2,所以圆心C(1,2)或(2,1).

练习册系列答案
相关题目