题目内容
已知等差数列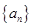 满足:
满足: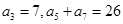 .
.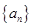 的前
的前 项和为
项和为 。
。
(Ⅰ)求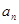 及
及 ;
;
(Ⅱ)令 ,求数列
,求数列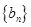 的前
的前 项和
项和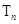 .
.
(Ⅰ) ,
,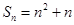 ;(Ⅱ)
;(Ⅱ)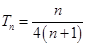 .
.
解析试题分析:(Ⅰ)因为数列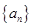 为等差数列,可由等差数列的通项公式
为等差数列,可由等差数列的通项公式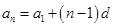 ,可将已知条件
,可将已知条件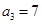 ,
,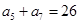 转化为关于首项
转化为关于首项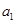 ,公差
,公差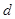 的二元一次方程
的二元一次方程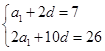 ,求出
,求出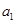 与
与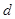 的值,从而求出通项
的值,从而求出通项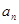 及前
及前 和
和 ;(Ⅱ)由(Ⅰ)得
;(Ⅱ)由(Ⅰ)得 ,所以可得数列
,所以可得数列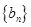 的通项
的通项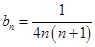 ,观察其通项特点
,观察其通项特点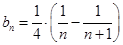 ,可采用裂项相消法来求其前
,可采用裂项相消法来求其前 项和
项和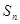 (裂项相消法在求前
(裂项相消法在求前 项和中常用的一种方法,其特点是通项公式可裂开成两项之差,相加后可以消掉中间项).
项和中常用的一种方法,其特点是通项公式可裂开成两项之差,相加后可以消掉中间项).
试题解析:(Ⅰ)设等差数列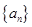 的首项为
的首项为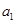 ,公差为
,公差为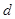 ,
,
由于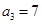 ,
,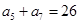 ,
,
所以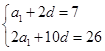 ,解得
,解得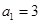 ,
,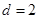 .
.
由于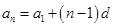 ,
, ,
,
所以 ,
,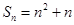 .
.
(Ⅱ)因为 ,所以
,所以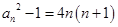 ,
, .
.
因此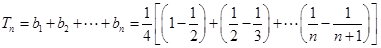 =
= .
.
所以数列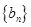 的前
的前 项和
项和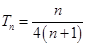 .
.
考点:1.等差数列;2.数列前 项和.
项和.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
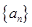 的前
的前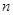 项和为
项和为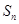 ,满足
,满足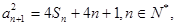 且
且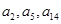 恰好是等比数列
恰好是等比数列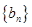 的前三项.
的前三项. ,若对任意的
,若对任意的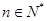 ,
,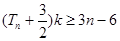 恒成立,求实数
恒成立,求实数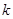 的取值范围.
的取值范围.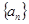 为等差数列,且
为等差数列,且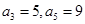 ;数列
;数列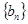 的前n项和为
的前n项和为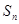 ,且
,且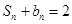 。
。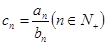 ,
,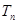 为数列
为数列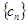 的前n项和,求
的前n项和,求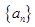 中,已知
中,已知 ,
,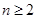 时,
时,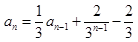 .数列
.数列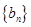 满足:
满足: .
.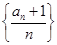 的前
的前 项和为
项和为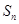 ,若不等式
,若不等式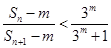 成立(
成立(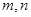 为正整数).求出所有符合条件的有序实数对
为正整数).求出所有符合条件的有序实数对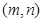 .
.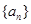 的前
的前 项和为
项和为 ,且
,且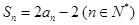 ,数列
,数列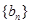 满足
满足 ,且
,且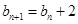 .
. 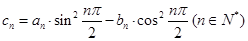 ,求数列
,求数列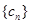 的前
的前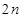 项和
项和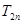 .
.  满足
满足 ,且对任意非负整数
,且对任意非负整数 均有:
均有: .
. ;
; 是等差数列,并求
是等差数列,并求 的通项;
的通项; ,求证:
,求证: .
.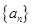 的前
的前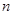 项和为
项和为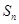 ,且
,且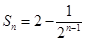 .
.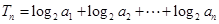 ,求证:
,求证: .
.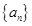 ,等比数列
,等比数列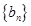 中,
中,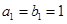 ,
,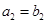 ,
,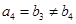 .
.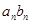 ;
;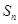 为数列
为数列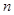 项和,
项和,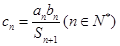 ,
,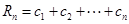 ,求
,求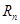 .
.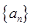 是首项为
是首项为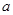 ,公差为
,公差为 的等差数列
的等差数列 ,
, 是其前
是其前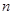 项和.
项和. ,
, ,求数列
,求数列 ,
, ,且
,且 、
、 、
、 成等比数列,证明:
成等比数列,证明: .
.