题目内容
数列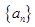 中,已知
中,已知 ,
,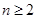 时,
时,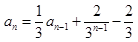 .数列
.数列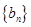 满足:
满足: .
.
(1)证明: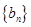 为等差数列,并求
为等差数列,并求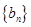 的通项公式;
的通项公式;
(2)记数列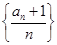 的前
的前 项和为
项和为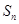 ,若不等式
,若不等式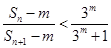 成立(
成立(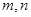 为正整数).求出所有符合条件的有序实数对
为正整数).求出所有符合条件的有序实数对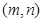 .
.
(1)通项公式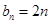 ,(2) 有序实数对
,(2) 有序实数对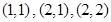
解析试题分析:(1)由等差数列的定义证明,当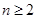 时,
时,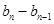 经过整理为一个常数,从而得出它的公差,进一步得出它的通项公式.
经过整理为一个常数,从而得出它的公差,进一步得出它的通项公式.
(2)利用(1)的结论, 可得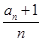 表示的式子,经判断
表示的式子,经判断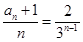 为等比数列,利用等比数列的前n项和公式求出
为等比数列,利用等比数列的前n项和公式求出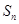 ,表示出
,表示出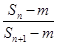 为多少,利用不等式得出m的范围,进一步得出有序实数对.
为多少,利用不等式得出m的范围,进一步得出有序实数对.
试题解析:(Ⅰ)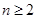 时,
时,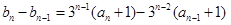 , 2分
, 2分
代入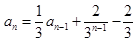 整理得
整理得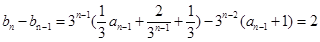 ,
,
故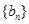 是公差为
是公差为 的等差数列. 6分
的等差数列. 6分
通项公式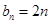
(Ⅱ)由(Ⅰ)得,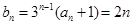 ,故
,故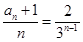 ,所以
,所以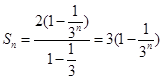 8分
8分
则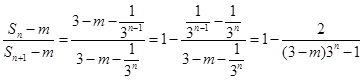 10分
10分
因为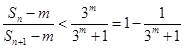 ,得
,得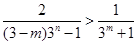 11分
11分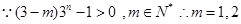 12分
12分
当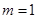 时,
时,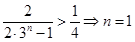 ;当
;当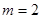 时,
时,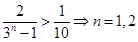 13分
13分
综上,存在符合条件的所有有序实数对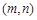 为:
为: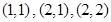 . 14分
. 14分
考点:等差数列,等比数列,不等式.

练习册系列答案
相关题目
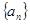 和等比数列
和等比数列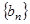 中,
中,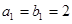 ,
,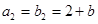 ,
,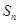 是
是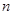 项和.
项和. 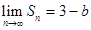 ,求实数
,求实数 的值;
的值;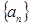 中?若存在,求出所有的
中?若存在,求出所有的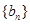 中至少有三项在数列
中至少有三项在数列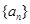 中,但
中,但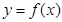 确定数列
确定数列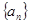 ,
,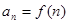 .若函数
.若函数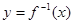 能确定数列
能确定数列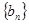 ,
,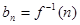 ,则称数列
,则称数列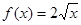 确定数列
确定数列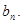 ;
;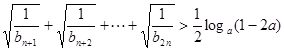 对任意的正整数
对任意的正整数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;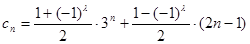 (
( 为正整数),若数列
为正整数),若数列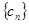 的反数列为
的反数列为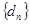 ,
,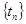 (公共项
(公共项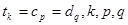 为正整数),求数列
为正整数),求数列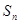 .
. 的三边长
的三边长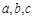 ,满足
,满足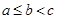
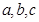 均为正整数,且
均为正整数,且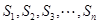 ,且
,且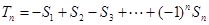 ,求满足不等式
,求满足不等式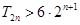 的所有
的所有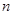 的值;
的值;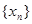 满足
满足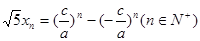 ,证明数列
,证明数列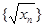 中的任意连续三项为边长均可以构成直角三角形,且
中的任意连续三项为边长均可以构成直角三角形,且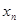 是正整数.
是正整数.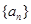 是公差大于零的等差数列,已知
是公差大于零的等差数列,已知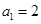 ,
,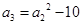 .
.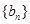 是以函数
是以函数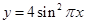 的最小正周期为首项,以
的最小正周期为首项,以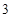 为公比的等比数列,求数列
为公比的等比数列,求数列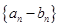 的前
的前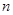 项和
项和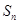 .
.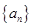 满足:
满足: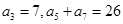 .
. 项和为
项和为 。
。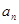 及
及 ,求数列
,求数列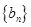 的前
的前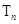 .
.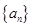 的前3项和
的前3项和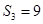 ,且
,且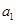 、
、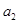 、
、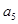 成等比数列.
成等比数列.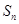 ;
;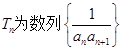 的前n项和,证明:
的前n项和,证明: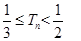 ;
; ,若
,若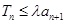 对一切
对一切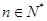 恒成立,求实数
恒成立,求实数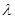 的最小值.
的最小值.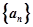 的前n项和为
的前n项和为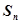 ,且
,且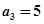 ,
, .
. 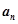 ;
; ,求数列
,求数列 的前n项和
的前n项和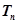 .
.