题目内容
(本小题满分12分)
已知函数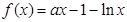
 .
.
(Ⅰ)讨论函数 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(Ⅱ)若函数 在
在 处取得极值,对
处取得极值,对
 ,
, 恒成立,
恒成立,
求实数 的取值范围;
的取值范围;
(Ⅲ)当 且
且 时,试比较
时,试比较 的大小.
的大小.
(Ⅰ)当 时
时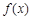 在
在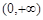 上没有极值点,当
上没有极值点,当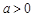 时,
时,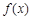 在
在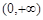 上有一个极值点(Ⅱ)
上有一个极值点(Ⅱ)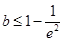 (Ⅲ)当
(Ⅲ)当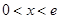 时,
时,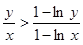 ,当
,当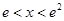 时,
时,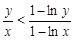 .
.
解析试题分析:(Ⅰ)由已知得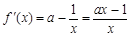 ,
,
所以当 时,
时,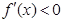 在
在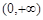 上恒成立,函数
上恒成立,函数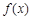 在
在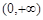 单调递减,
单调递减,
∴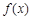 在
在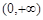 上没有极值点;
上没有极值点;
当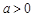 时,由
时,由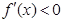 得
得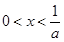 ,
,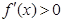 得
得 ,
,
∴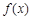 在
在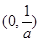 上递减,在
上递减,在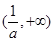 上递增,即
上递增,即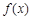 在
在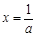 处有极小值.
处有极小值.
∴当 时
时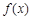 在
在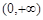 上没有极值点,
上没有极值点,
当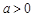 时,
时,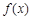 在
在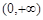 上有一个极值点. ……3分
上有一个极值点. ……3分
(Ⅱ)∵函数 在
在 处取得极值,∴
处取得极值,∴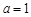 ,
,
∴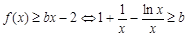 , ……5分
, ……5分
令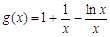 ,可得
,可得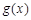 在
在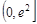 上递减,在
上递减,在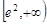 上递增,
上递增,
∴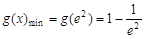 ,即
,即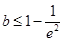 . ……7分
. ……7分
(Ⅲ)由(Ⅱ)知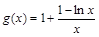 在(0,e2)上单调减,
在(0,e2)上单调减,
∴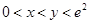 时,
时,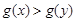 ,
,
即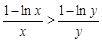 .
.
当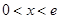 时,
时,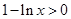 ,∴
,∴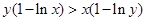 , ∴
, ∴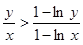 ,
,
当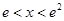 时,
时,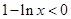 ,∴
,∴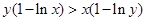 , ∴
, ∴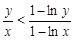 .
.
……12分
考点:本小题主要考查利用导数判断极值点的个数、利用导数解决恒成立问题和利用导数证明不等式等问题,考生学生的逻辑思维能力和运算求解能力.
点评:导数是研究函数性质的一个比较好的工具,给出函数可以利用导数考查函数的性质,恒成立问题可以转化为最值问题来解决,如果最值不好求,可以构造新函数再次利用导数求解,一定要灵活运用导数,使导数的功能完全发挥出来.

练习册系列答案
相关题目
 .
.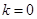 ,求
,求 的最小值;
的最小值;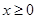 时
时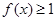 ,求实数
,求实数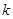 的取值范围.
的取值范围.
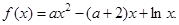
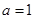 时,求曲线
时,求曲线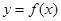 在点
在点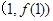 处的切线方程;
处的切线方程;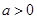 时,若
时,若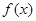 在区间
在区间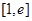 上的最小值为-2,求
上的最小值为-2,求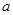 的取值范围;
的取值范围;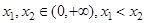 ,且
,且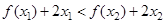 恒成立,求
恒成立,求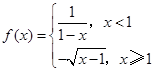 ,
,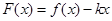 ,x∈R.试讨论函数F(x)的单调性.
,x∈R.试讨论函数F(x)的单调性. 
 ,试确定函数
,试确定函数 的单调区间;
的单调区间; ,且对于任意
,且对于任意 ,
, 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;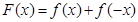 ,求证:
,求证: .
.  的图像与直线
的图像与直线 相切于点
相切于点 .
. 的值;
的值; 的单调性.
的单调性.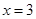 是函数
是函数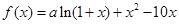 的一个极值点。
的一个极值点。 ;
;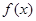 的单调区间;
的单调区间;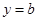 与函数
与函数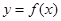 的图象有3个交点,求
的图象有3个交点,求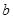 的取值范围。
的取值范围。 ,
, 
 时, 若
时, 若 有
有 个零点, 求
个零点, 求 的取值范围;
的取值范围; , 当
, 当 时恒有
时恒有 , 求
, 求 的最大值, 并求此时
的最大值, 并求此时