题目内容
(本小题满分12分)
设函数 的图像与直线
的图像与直线 相切于点
相切于点 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)讨论函数 的单调性.
的单调性.
(Ⅰ)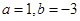 .
.
(Ⅱ)故当x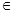 (
(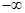 , -1)时,f(x)是增函数,当 x
, -1)时,f(x)是增函数,当 x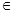 (3,
(3,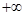 )时,f(x)也是增函数,
)时,f(x)也是增函数,
当x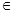 (-1 ,3)时,f(x)是减函数.
(-1 ,3)时,f(x)是减函数.
解析试题分析:(I)由于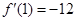 和函数f(x)过点(1,-11)可建立关于a,b的方程求出a,b的值.
和函数f(x)过点(1,-11)可建立关于a,b的方程求出a,b的值.
(II)根据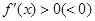 可求得函数f(x)的单调递增(减)区间.
可求得函数f(x)的单调递增(减)区间.
(Ⅰ)求导得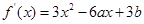 . -------------------2分
. -------------------2分
由于  的图像与直线
的图像与直线 相切于点
相切于点 ,
,
所以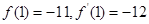 , -------------- 4分
, -------------- 4分
即:  1-3a+3b = -11 解得:
1-3a+3b = -11 解得: 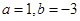 . -------------------- 6分
. -------------------- 6分
3-6a+3b=-12
(Ⅱ)由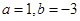 得:
得: ------------ 8分
------------ 8分
令f′(x)>0,解得 x<-1或x>3;
又令f′(x)< 0,解得 -1<x<3. ------ 10分
故当x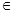 (
(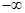 , -1)时,f(x)是增函数,当 x
, -1)时,f(x)是增函数,当 x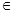 (3,
(3,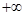 )时,f(x)也是增函数,
)时,f(x)也是增函数,
当x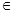 (-1 ,3)时,f(x)是减函数. --------------------- 12分
(-1 ,3)时,f(x)是减函数. --------------------- 12分
考点:导数的几何意义,利用导数求函数的极大值.
点评:在某点处的导数就是在此点处的切线的斜率,利用导数大(小)零解不等式可得函数的单调递增(减)区间.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 (a为实常数).
(a为实常数).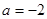 ,求证:函数
,求证:函数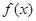 在(1,+.∞)上是增函数;
在(1,+.∞)上是增函数;  值;
值;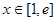 ,使得
,使得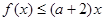 成立,求实数a的取值范围.
成立,求实数a的取值范围. ,函数
,函数 的最小值为
的最小值为 ,
, 时,求
时,求 同时满足下列条件:①
同时满足下列条件:① ;②当
;②当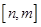 时,值域为
时,值域为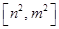
 ?若存在,求出
?若存在,求出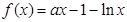
 .
. 在定义域内的极值点的个数;
在定义域内的极值点的个数; 处取得极值,对
处取得极值,对
 ,
, 恒成立,
恒成立, 的取值范围;
的取值范围; 且
且 时,试比较
时,试比较 的大小.
的大小. 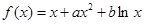 ,曲线
,曲线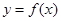 过点
过点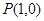 ,且在
,且在 点处的切线斜率为2.
点处的切线斜率为2.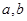 的值;
的值;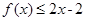
 ,在
,在 与
与 时,都取得极值。
时,都取得极值。 的值;
的值; 都有
都有 恒成立,求c的取值范围。
恒成立,求c的取值范围。 ②
② 
 (Ⅰ) 当
(Ⅰ) 当 时,求函数
时,求函数 的极值;
的极值; 时,讨论函数
时,讨论函数 及任意
及任意 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围.