题目内容
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE= ![]() BB1 , C1F=
BB1 , C1F= ![]() CC1 .
CC1 . 
(1)求平面AEF与平面ABC所成角α的余弦值;
(2)若G为BC的中点,A1G与平面AEF交于H,且设 ![]() =
= ![]() ,求λ的值.
,求λ的值.
【答案】
(1)解:在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE= ![]() BB1,C1F=
BB1,C1F= ![]() CC1.
CC1.
∴建立以A为坐标原点,AB,AC,AA1分别为x,y,z轴的空间直角坐标系如图:
则A(0,0,0),A1(0,0,6),B(2,0,0),C(0,2,0),E(2,0,2),F(0,2,4),
则 ![]() =(2,0,2),
=(2,0,2), ![]() =(0,2,4),
=(0,2,4),
设平面AEF的法向量为 ![]() =(x,y,z)
=(x,y,z)
则 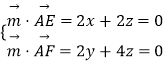
令z=1.则x=﹣1,y=﹣2,
即 ![]() =(﹣1,﹣2,1),
=(﹣1,﹣2,1),
平面ABC的法向量为 ![]() =(0,0,1),
=(0,0,1),
则cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]()
即平面AEF与平面ABC所成角α的余弦值是 ![]()
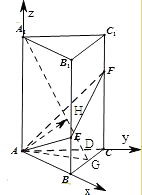
(2)解:若G为BC的中点,A1G与平面AEF交于H,
则G(1,1,0),
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =λ(1,1,﹣6)=(λ,λ,﹣6λ),
=λ(1,1,﹣6)=(λ,λ,﹣6λ),
![]() =
= ![]() +
+ ![]() =(λ,λ,6﹣6λ)
=(λ,λ,6﹣6λ)
∵A,E,F,H四点共面,
∴设 ![]() =x
=x ![]() +y
+y ![]() ,
,
即(λ,λ,6﹣6λ)=x(2,0,2)+y(0,2,4),
则 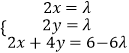 ,得λ=
,得λ= ![]() ,x=y=
,x=y= ![]() ,
,
故λ的值为 ![]() .
.
【解析】(1)建立空间坐标系,求出平面的法向量,利用向量法进行求解即可.(2)利用四点共面, ![]() =x
=x ![]() +y
+y ![]() ,建立方程关系进行求解即可.
,建立方程关系进行求解即可.
【考点精析】认真审题,首先需要了解棱柱的结构特征(两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形).

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案