题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
解析:(1)方法一 取PC中点G,连结FG、EG,则FG∥CD,且FG= ∴FG平行等于AE,∴四边形AEGF是平行四边形,则AF∥EG.∵EG 方法二 取CD中点M,连结FM、AM,再证平面AMF∥平面PFC,而AF 点评:求点面距离的关键是作垂线时确定垂足的位置,一般要利用面面垂直的性质. |
(2) |
证CD⊥平面PAD,∴∠PDA就是二面角P-CD-B的平面角,∴∠PDA= 又EG 在Rt△PFG中,FH= 点评:本题也可用“三棱锥体积法”,即利用三棱锥可换底的特征,即由VF-PEC=VE-PFC来求,也可以先转化为求A到平面PEC的距离,再利用VA-PEC=VP-AEC来求. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
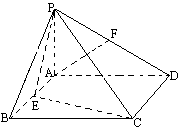
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.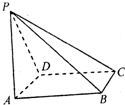 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,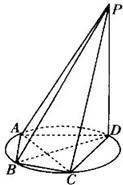 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.