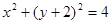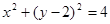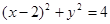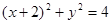题目内容
已知曲线C:
,直线l:ρ(cosθ-2sinθ)=12.
(1)将直线l的极坐标方程化为直角坐标方程;
(2)设点P在曲线C上,求P点到直线l距离的最小值.
|
(1)将直线l的极坐标方程化为直角坐标方程;
(2)设点P在曲线C上,求P点到直线l距离的最小值.
(1)∵ρ(cosθ-2sinθ)=12,
∴ρcosθ-2ρsinθ=12,
即:x-2y-12=0;
∴直线l的极坐标方程化为直角坐标方程为x-2y-12=0(4分)
(2)设P(3cosθ,2sinθ),
∴d=
=
|5cos(θ+φ)-12|
(其中,cosφ=
,sinφ=
)
当cos(θ+φ)=1时,dmin=
,
∴P点到直线l的距离的最小值为
.(10分)
∴ρcosθ-2ρsinθ=12,
即:x-2y-12=0;
∴直线l的极坐标方程化为直角坐标方程为x-2y-12=0(4分)
(2)设P(3cosθ,2sinθ),
∴d=
| |3cosθ-4sinθ-12| | ||
|
| ||
| 5 |
(其中,cosφ=
| 3 |
| 5 |
| 4 |
| 5 |
当cos(θ+φ)=1时,dmin=
7
| ||
| 5 |
∴P点到直线l的距离的最小值为
7
| ||
| 5 |

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
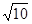 ,0)作直线l,交曲线
,0)作直线l,交曲线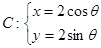 (θ为参数)于A,B两点,若|MA|,|AB|,|MB|成等比数列,求直线l的方程.
(θ为参数)于A,B两点,若|MA|,|AB|,|MB|成等比数列,求直线l的方程.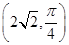 作圆
作圆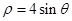 的切线,则切线的极坐标方程是 .
的切线,则切线的极坐标方程是 .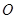 的半径为
的半径为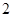 ,圆
,圆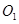 ,
,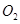 ,
,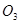 为球
为球 ,
,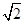 ,
,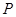 ,则
,则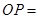
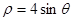 化为直角坐标为 ( )
化为直角坐标为 ( )