题目内容
8.设全集U=R,集合A={x|2x-2>0},B={x|x2-x-2<0},求∁UA,∁UB,A∩B,∁U(A∩B).分析 根据已知中全集U=R,集合A={x|2x-2>0},B={x|x2-x-2<0},结合集合交集,并集,补集的定义,可得答案.
解答 解:∵全集U=R,集合A={x|2x-2>0}=(1,+∞),
B={x|x2-x-2<0}=(-1,2),
∴∁UA=(-∞,1],
∁UB=(-∞,-1]∪[2,+∞),
A∩B=(1,2),
∁U(A∩B)(-∞,1]∪[2,+∞).
点评 本题考查的知识点是集合的交集,并集,补集运算,难度不大,属于基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
10.若α是第三象限的角,则$\frac{1}{2}$α是( )
| A. | 第一、三象限角 | B. | 第一、二象限角 | C. | 第二、三象限角 | D. | 第二、四象限角 |
7.若集合A={x|-2<x<1},B={x|0<x<2},则集合A∩B=( )
| A. | { x|-1<x<1} | B. | { x|-2<x<1} | C. | { x|-2<x<2} | D. | { x|0<x<1} |
8.$\int_1^2{(x-\frac{1}{x})}dx$的值是( )
| A. | 0 | B. | 1.5-ln2 | C. | 3-ln2 | D. | 1 |
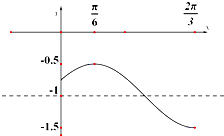 如果函数y=Asin(ωx+φ)+B(A>0,|φ|<$\frac{π}{2}$)的一段图象.
如果函数y=Asin(ωx+φ)+B(A>0,|φ|<$\frac{π}{2}$)的一段图象.