题目内容
与双曲线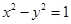
过一、三象限的渐近线平行且距离为
的直线方程为 .
；
解析试题分析：双曲线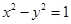过一、三象限的渐近线方程为：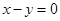
设直线方程为：
所以
，解得
考点：双曲线的性质、直线方程和两平行直线减的距离.
练习册系列答案
发散思维新课堂系列答案
相关题目
发散思维新课堂系列答案题目内容
与双曲线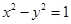过一、三象限的渐近线平行且距离为的直线方程为 .
；
解析试题分析：双曲线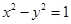过一、三象限的渐近线方程为：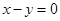
设直线方程为：所以，解得
考点：双曲线的性质、直线方程和两平行直线减的距离.
发散思维新课堂系列答案
且和抛物线
相切的直线
方程为 .
绕
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是 ．
的一条渐近线方程为
，则该双曲线的离心率为 ．
的虚轴长是实轴长的2倍，则m= .
的焦点到渐近线的距离等于 ．
的弦被点
平分，则此弦所在直线的斜率为 
的左顶点A且斜率为
的直线交椭圆
于另一点
，且点
轴上的射影恰为右焦点
,若
，则椭圆的离心率
的取值范围是 .