题目内容
数列{an}的前n项和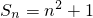 .
.
(1)求数列{an}的通项公式;
(2)设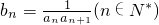 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
解:(1)由已知:当n=1时a1=s1=2
当n≥2时an=sn-sn-1=2n-1
∴数列{an}的通项公式为an=
(2)由(1)知:bn=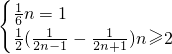
当n=1时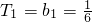
当n≥2时
Tn=b1+b2+…+bn
= +2(
+2( )
)
=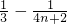
∴数列{bn}的前n项和Tn=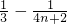
分析:(1)利用n≥2时an=sn-sn-1求出an(n≥2)的表达式然后利用a1=s1求出a1然后看其是否适合an(n≥2)的表达式,若适合则两则合二为一,若不适合则写成分段函数的形式.
(1)根据(1)可得bn=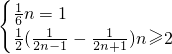 再代入Tn=b1+b2+…+bn即可得解.
再代入Tn=b1+b2+…+bn即可得解.
点评:本题主要考查了数列通项公式的求解以及数列的求和,属常考题,较难.解题的关键是对于已知sn求an需利用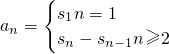 进行求解,而对于数列{bn}的前n项的求解方法--裂项相消法要引起以后学习的注意!
进行求解,而对于数列{bn}的前n项的求解方法--裂项相消法要引起以后学习的注意!
当n≥2时an=sn-sn-1=2n-1
∴数列{an}的通项公式为an=

(2)由(1)知:bn=
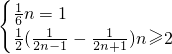
当n=1时
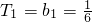
当n≥2时
Tn=b1+b2+…+bn
=
 +2(
+2( )
)=
∴数列{bn}的前n项和Tn=
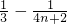
分析:(1)利用n≥2时an=sn-sn-1求出an(n≥2)的表达式然后利用a1=s1求出a1然后看其是否适合an(n≥2)的表达式,若适合则两则合二为一,若不适合则写成分段函数的形式.
(1)根据(1)可得bn=
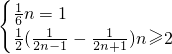 再代入Tn=b1+b2+…+bn即可得解.
再代入Tn=b1+b2+…+bn即可得解.点评:本题主要考查了数列通项公式的求解以及数列的求和,属常考题,较难.解题的关键是对于已知sn求an需利用
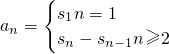 进行求解,而对于数列{bn}的前n项的求解方法--裂项相消法要引起以后学习的注意!
进行求解,而对于数列{bn}的前n项的求解方法--裂项相消法要引起以后学习的注意! 
练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目