题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】(1)当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,无单调递减区间;当
,无单调递减区间;当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,
,![]() ,单调递减区间是
,单调递减区间是![]() ;当
;当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,
,![]() ,单调递减区间是
,单调递减区间是![]() ;(2)
;(2)![]() .
.
【解析】
(1)对![]() 求导,对参数
求导,对参数![]() 进行分类讨论,即可求得函数的单调性;
进行分类讨论,即可求得函数的单调性;
(2)分离参数,根据![]() 的取值不同,进行分类讨论,将问题转化为函数最值的问题进行处理.
的取值不同,进行分类讨论,将问题转化为函数最值的问题进行处理.
(1)![]()
当![]() 即
即![]() 时,
时,![]()
当![]() 即
即![]() 时,由
时,由![]() 得
得![]() 或
或![]() ;由
;由![]() 得
得![]()
当![]() 即
即![]() 时,由
时,由![]() 得
得![]() 或
或![]() ;由
;由![]() 得
得![]()
综上:
当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,无单调递减区间
,无单调递减区间
当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,
,![]() ,
,
单调递减区间是![]()
当![]() 时,
时,![]() 的单调递增区间是
的单调递增区间是![]() ,
,![]() ,
,
单调递减区间是![]()
(2)![]()
①当![]() 时,
时,![]() 成立,故
成立,故![]()
②当![]() 即
即![]() 时,
时,![]()
令![]() ,即求
,即求![]() 在
在![]() 上的最大值
上的最大值
∵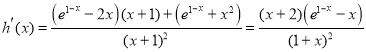
令![]() 则
则![]() 在
在![]() 上为减函数,且
上为减函数,且![]()
故当![]() 时,
时,![]() ,
,![]() 时,
时,![]()
故![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减
上单调递减
∴![]() 在
在![]() 上的最大值为
上的最大值为![]()
∴![]()
③当![]() 时,
时,![]()
即求![]() 在
在![]() 上的最小值
上的最小值
∵![]() 时,
时,![]() ,
,![]() 时,
时,![]()
∴![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增
上单调递增
∴![]() 在
在![]() 上的最小值为
上的最小值为![]()
∴![]() .
.
∴综上,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】每年9月第三周是国家网络安全宣传周.某学校为调查本校学生对网络安全知识的了解情况,组织了《网络信息辨析测试》活动,并随机抽取50人的测试成绩绘制了频率分布直方图如图所示:

(1)某学生的测试成绩是75分,你觉得该同学的测试成绩低不低?说明理由;
(2)将成绩在![]() 内定义为“合格”;成绩在
内定义为“合格”;成绩在![]() 内定义为“不合格”.①请将下面的
内定义为“不合格”.①请将下面的![]() 列联表补充完整; ②是否有90%的把认为网络安全知识的掌握情况与性别有关?说明你的理由;
列联表补充完整; ②是否有90%的把认为网络安全知识的掌握情况与性别有关?说明你的理由;
合格 | 不合格 | 合计 | |
男生 | 26 | ||
女生 | 6 | ||
合计 |
(3)在(2)的前提下,对50人按是否合格,利用分层抽样的方法抽取5人,再从5人中随机抽取2人,求恰好2人都合格的概率.附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.