题目内容
对于定义域为D的函数y=f(x),若有常数M,使得对任意的x1∈D,存在唯一的x2∈D满足等式 ,则称M为函数y=f (x)的“均值”.
,则称M为函数y=f (x)的“均值”.(1)判断1是否为函数f(x)=2x+1(-1≤x≤1)的“均值”,请说明理由;
(2)若函数f(x)=ax2-2x(1<x<2,a为常数)存在“均值”,求实数a的取值范围;
(3)若函数f(x)是单调函数,且其值域为区间I.试探究函数f(x)的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
【答案】分析:(1)根据均值的定义,要判断1是函数f(x)=2x+1(-1≤x≤1)的“均值”,即要验证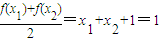 ;
;
(2)函数f(x)=ax2-2x(1<x<2,a为常数)存在“均值”,当a=0时,f(x)=-2x(1<x<2)存在“均值”,且“均值”为-3;当a≠0时,由f(x)=ax2-2x(1<x<2)存在均值,可知对任意的x1,都有唯一的x2与之对应,从而有f(x)=ax2-2x(1<x<2)单调,从而求得实数a的取值范围;
(3)根据(1),(2)的结论对于当I=(a,b)或[a,b]时,函数f(x)存在唯一的“均值”;当I为(-∞,+∞)时,函数f(x)存在无数多个“均值”,当为半开半闭区间时,函数f(x)不存在均值.
解答:解:(1)对任意的x1∈[-1,1],有-x1∈[-1,1],
当且仅当x2=-x1时,有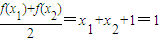 ,
,
故存在唯一x2∈[-1,1],满足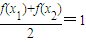 ,
,
所以1是函数f(x)=2x+1(-1≤x≤1)的“均值”.
(2)当a=0时,f(x)=-2x(1<x<2)存在“均值”,且“均值”为-3;
当a≠0时,由f(x)=ax2-2x(1<x<2)存在均值,可知对任意的x1,
都有唯一的x2与之对应,从而有f(x)=ax2-2x(1<x<2)单调,
故有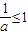 或
或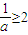 ,
,
解得a≥1或a<0或 ,
,
综上,a的取值范围是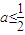 或a≥1.
或a≥1.
(3)①当I=(a,b)或[a,b]时,函数f(x)存在唯一的“均值”.
这时函数f(x)的“均值”为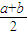 ;
;
②当I为(-∞,+∞)时,函数f(x)存在无数多个“均值”.
这时任意实数均为函数f(x)的“均值”;
③当I=(a,+∞)或(-∞,a)或[a,+∞)或(-∞,a]或[a,b)或(a,b]时,
函数f(x)不存在“均值”.
①当且仅当I形如(a,b)、[a,b]其中之一时,函数f(x)存在唯一的“均值”.
这时函数f(x)的“均值”为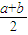 ;
;
②当且仅当I为(-∞,+∞)时,函数f(x)存在无数多个“均值”.
这时任意实数均为函数f(x)的“均值”;
③当且仅当I形如(a,+∞)、(-∞,a)、[a,+∞)、(-∞,a]、[a,b)、(a,b]其中之一时,
函数f(x)不存在“均值”.
点评:此题是个中档题,考查函数单调性的理解,和学生的阅读能力,以及分析解决问题的能力,其中问题(3)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.
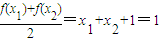 ;
;(2)函数f(x)=ax2-2x(1<x<2,a为常数)存在“均值”,当a=0时,f(x)=-2x(1<x<2)存在“均值”,且“均值”为-3;当a≠0时,由f(x)=ax2-2x(1<x<2)存在均值,可知对任意的x1,都有唯一的x2与之对应,从而有f(x)=ax2-2x(1<x<2)单调,从而求得实数a的取值范围;
(3)根据(1),(2)的结论对于当I=(a,b)或[a,b]时,函数f(x)存在唯一的“均值”;当I为(-∞,+∞)时,函数f(x)存在无数多个“均值”,当为半开半闭区间时,函数f(x)不存在均值.
解答:解:(1)对任意的x1∈[-1,1],有-x1∈[-1,1],
当且仅当x2=-x1时,有
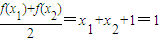 ,
,故存在唯一x2∈[-1,1],满足
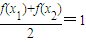 ,
,所以1是函数f(x)=2x+1(-1≤x≤1)的“均值”.
(2)当a=0时,f(x)=-2x(1<x<2)存在“均值”,且“均值”为-3;
当a≠0时,由f(x)=ax2-2x(1<x<2)存在均值,可知对任意的x1,
都有唯一的x2与之对应,从而有f(x)=ax2-2x(1<x<2)单调,
故有
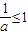 或
或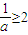 ,
,解得a≥1或a<0或
 ,
,综上,a的取值范围是
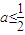 或a≥1.
或a≥1. (3)①当I=(a,b)或[a,b]时,函数f(x)存在唯一的“均值”.
这时函数f(x)的“均值”为
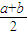 ;
; ②当I为(-∞,+∞)时,函数f(x)存在无数多个“均值”.
这时任意实数均为函数f(x)的“均值”;
③当I=(a,+∞)或(-∞,a)或[a,+∞)或(-∞,a]或[a,b)或(a,b]时,
函数f(x)不存在“均值”.
①当且仅当I形如(a,b)、[a,b]其中之一时,函数f(x)存在唯一的“均值”.
这时函数f(x)的“均值”为
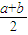 ;
; ②当且仅当I为(-∞,+∞)时,函数f(x)存在无数多个“均值”.
这时任意实数均为函数f(x)的“均值”;
③当且仅当I形如(a,+∞)、(-∞,a)、[a,+∞)、(-∞,a]、[a,b)、(a,b]其中之一时,
函数f(x)不存在“均值”.
点评:此题是个中档题,考查函数单调性的理解,和学生的阅读能力,以及分析解决问题的能力,其中问题(3)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

练习册系列答案
相关题目