题目内容
直线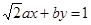 与圆
与圆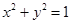 相交于
相交于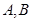 两点(其中
两点(其中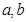 是实数),且
是实数),且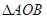 是直角三角形(
是直角三角形(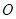 是坐标原点),则点
是坐标原点),则点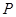
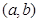 与点
与点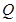
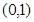 之间距离的最大值为 ( )
之间距离的最大值为 ( )
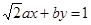 与圆
与圆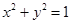 相交于
相交于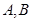 两点(其中
两点(其中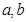 是实数),且
是实数),且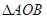 是直角三角形(
是直角三角形(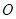 是坐标原点),则点
是坐标原点),则点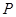
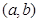 与点
与点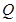
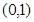 之间距离的最大值为 ( )
之间距离的最大值为 ( )A.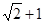 | B.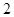 | C. | D.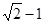 |
A
试题分析:由圆x2+y2=1,所以圆心(0,0),半径为1,所以|OA|=|OB|=1,则△AOB是等腰直角三角形,得到|AB|=
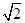 ,则圆心(0,0)到直线
,则圆心(0,0)到直线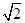 ax+by=1的距离为d=
ax+by=1的距离为d=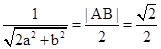 ,∴2a2+b2=2,即a2+
,∴2a2+b2=2,即a2+
因此所求距离为椭圆a2+
 上点P(a,b)到焦点(0,1)的距离,如图
上点P(a,b)到焦点(0,1)的距离,如图
得到其最大值PF=
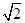 +1,故选A
+1,故选A点评:根据圆的方程找出圆心坐标和半径,由|OA|=|OB|根据题意可知△AOB是等腰直角三角形,根据勾股定理求出|AB|的长度,根据等腰直角三角形的性质可得圆心到直线的距离等于|AB|的一半,然后利用点到直线的距离公式表示出圆心到直线的距离,两者相等即可得到a与b的轨迹方程为一个椭圆,由图形可知点P(a,b)到焦点(0,1)的距离的最大值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
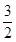 )2+y2=
)2+y2=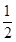
 ,则直线
,则直线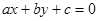 被圆
被圆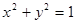 所截得的弦长为( )
所截得的弦长为( ) 

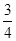
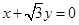 绕原点按顺时针方向旋转
绕原点按顺时针方向旋转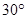 所得直线与圆
所得直线与圆 的位置关系是( ).
的位置关系是( ). 的位置关系是
的位置关系是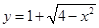 与直线
与直线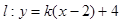 有两个不同的交点,实数
有两个不同的交点,实数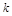 的范围是()
的范围是()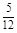 ,+∞)
,+∞)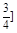
 ,
,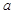 为任意实数时,直线
为任意实数时,直线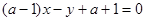 恒过定点
恒过定点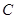 ,则以
,则以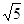 为半径的圆的方程是_____________.
为半径的圆的方程是_____________. 中,圆
中,圆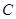 的方程为
的方程为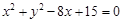 ,若直线
,若直线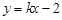 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆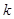 的取值范围是( )
的取值范围是( )
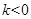 或
或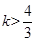
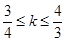
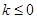 或
或