题目内容
定义在R上的函数f(x)满足f(x)-f(-x)=0,且对任意x,x∈[0,+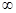 )(x
)(x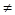 x),都有
x),都有 ,则
,则
A.f(3)<f(-2)<f(1) B.f(1)<f(-2)<f(3)
C.f(-2)<f(1)<f(3) D.f(3)<f(1)<f(-2)
【答案】
A
【解析】
试题分析:定义在R上的函数f(x)满足f(x)-f(-x)=0,因此可知函数是奇函数,则由对任意x,x∈[0,+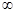 )(x
)(x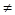 x),都有
x),都有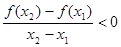 ,则可知函数在x>0上单调递减,可知x<0时,单调递减,而f(-2)=-f(2),结合函数对称性可知f(3)<f(-2)<f(1),故选A.
,则可知函数在x>0上单调递减,可知x<0时,单调递减,而f(-2)=-f(2),结合函数对称性可知f(3)<f(-2)<f(1),故选A.
考点:函数的奇偶性
点评:对于函数中点比较大小可知,只要确定出函数的单调性,然后结合性质得到结论。属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目