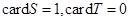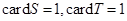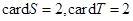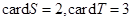题目内容
(5分)(2011•福建)在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],即[k]={5n+k丨n∈Z},k=0,1,2,3,4.给出如下四个结论:
①2011∈[1];
②﹣3∈[3];
③Z=[0]∪[1]∪[2]∪[3]∪[4];
④“整数a,b属于同一“类”的充要条件是“a﹣b∈[0]”.
其中,正确结论的个数是( )
| A.1 | B.2 | C.3 | D.4 |
C
解析试题分析:根据题中“类”的理解,在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,
对于各个结论进行分析:①∵2011÷5=402…1;②∵﹣3÷5=0…2,③整数集中的数被5除的数可以且只可以分成五类,故Z=[0]∪[1]∪[2]∪[3]∪[4];④从正反两个方面考虑即可.
解:①∵2011÷5=402…1,∴2011∈[1],故①对;
②∵﹣3=5×(﹣1)+2,∴对﹣3∉[3];故②错;
③∵整数集中的数被5除的数可以且只可以分成五类,故Z=[0]∪[1]∪[2]∪[3]∪[4],故③对;
④∵整数a,b属于同一“类”,∴整数a,b被5除的余数相同,从而a﹣b被5除的余数为0,反之也成立,故“整数a,b属于同一“类”的充要条件是“a﹣b∈[0]”.故④对.
∴正确结论的个数是3.
故选C.
点评:本题主要考查了选修3同余的性质,具有一定的创新,关键是对题中“类”的题解,属于创新题.

设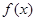 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当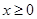 时,
时,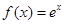 。若对任意的x
。若对任意的x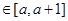 ,不等式
,不等式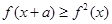 恒成立,则实数a的最大值是( )。
恒成立,则实数a的最大值是( )。
A.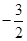 | B.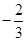 | C.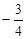 | D.2 |
已知函数 ,则下列说法错误的是( )
,则下列说法错误的是( )
A.若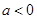 ,则 ,则 有零点 有零点 |
B.若 有零点,则 有零点,则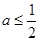 且 且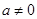 |
C.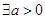 使得 使得 有唯一零点 有唯一零点 |
D.若 有唯一零点,则 有唯一零点,则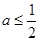 且 且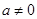 |
[2014·大庆质检]下列函数中,满足“对任意的x1,x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的是( )
A.f(x)= | B.f(x)=(x-1)2 |
| C.f(x)=ex | D.f(x)=ln(x+1) |
(2014·沈阳模拟)已知符号函数sgn(x)= 则函数f(x)=sgn(lnx)-lnx的零点个数为( )
则函数f(x)=sgn(lnx)-lnx的零点个数为( )
| A.1 | B.2 | C.3 | D.4 |
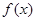 是定义在
是定义在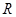 的奇函数,当
的奇函数,当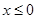 时,
时,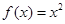 ,若对任意的
,若对任意的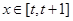 ,不等式
,不等式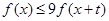 恒成立,则实数
恒成立,则实数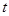 的最大值为( )
的最大值为( )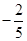
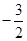
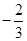
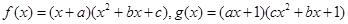 ,集合
,集合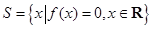 ,
,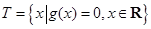 ,记
,记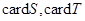 分别为集合
分别为集合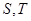 中的元素个数,那么下列结论不正确的是( )
中的元素个数,那么下列结论不正确的是( )