题目内容
设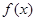 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当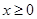 时,
时,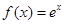 。若对任意的x
。若对任意的x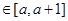 ,不等式
,不等式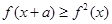 恒成立,则实数a的最大值是( )。
恒成立,则实数a的最大值是( )。
A.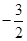 | B.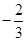 | C.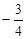 | D.2 |
C
解析试题分析: 是定义在
是定义在 上的偶函数,
上的偶函数,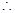 不等式
不等式 恒成立等价为
恒成立等价为 恒成立,
恒成立, 当
当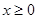 时,
时, .
.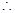 不等式等价为
不等式等价为 恒成立,
恒成立,
即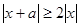 在
在 上恒成立,平方得
上恒成立,平方得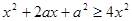
即 在
在 上恒成立,
上恒成立,
设 ,则满足
,则满足
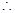 即
即
 故实数
故实数 的最大值是
的最大值是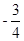 .故选C.
.故选C.
考点:1.函数的奇偶性;2.恒成立问题.

练习册系列答案
相关题目
函数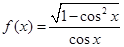 ( )
( )
A.在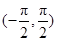 上递增 上递增 | B.在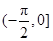 上递增,在 上递增,在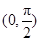 上递减 上递减 |
C.在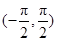 上递减 上递减 | D.在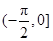 上递减,在 上递减,在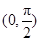 上递增 上递增 |
方程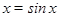 的解个数为( )
的解个数为( )
A.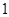 | B.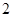 | C.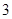 | D.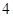 |
函数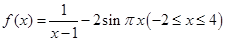 所有零点之和等于 ( ).
所有零点之和等于 ( ).
| A.2 | B.4 | C.6 | D.8 |
已知函数f(x)=loga(2x+b-1)(a>0,a≠1)的图象如图所示,则a,b满足的关系是( )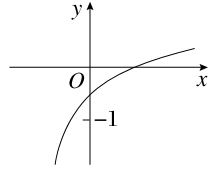
A.0<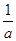 <b<1 <b<1 |
B.0<b<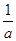 <1 <1 |
C.0<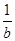 <a<1 <a<1 |
D.0<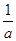 < <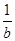 <1 <1 |
[2013·吉林调研]已知定义在R上的函数f(x)满足f(x)+f(-x)=0,且在(-∞,0)上单调递增,如果x1+x2<0且x1x2<0,则f(x1)+f(x2)的值( )
| A.可能为0 | B.恒大于0 |
| C.恒小于0 | D.可正可负 |
(2014·荆州模拟)函数y=ln(2-x-x2)+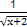 的定义域是( )
的定义域是( )
| A.(-1,2) | B.(-∞,-2)∪(1,+∞) |
| C.(-2,1) | D.[-2,1) |
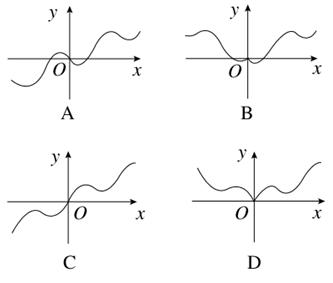
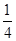 x2+sin(
x2+sin(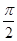 +x),f′(x)为f(x)的导函数,则f′(x)的图象是( )
+x),f′(x)为f(x)的导函数,则f′(x)的图象是( )