题目内容
已知数列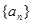 是公差不为零的等差数列,
是公差不为零的等差数列,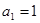 ,且
,且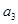 是
是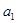 和
和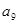 的等比中项.
的等比中项.
(1)求数列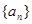 的通项公式;
的通项公式;
(2)设数列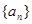 的前
的前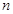 项和为
项和为 ,
,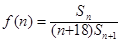 ,试问当
,试问当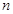 为何值时,
为何值时,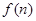 最大?并求出
最大?并求出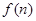 的最大值.
的最大值.
(1) 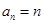 ;(2) 当且仅当
;(2) 当且仅当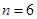 时,
时,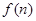 取得最大值
取得最大值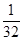 .
.
解析试题分析:(1) 设出等差数列 的公差
的公差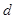 ,利用
,利用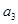 是
是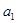 和
和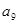 的等比中项列方程求出公差而得通项公式.
的等比中项列方程求出公差而得通项公式.
(2)根据等差数列的前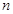 项和公式求出
项和公式求出 ,从而得出并化简
,从而得出并化简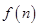 ,最后结合
,最后结合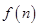 的特点,用函数的方法或不等式的方法求出的
的特点,用函数的方法或不等式的方法求出的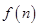 最大值.
最大值.
试题解析:解:(1)设等差数列 的公差为
的公差为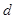 ,则
,则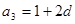
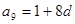 2分
2分
∵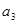 是
是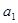 和
和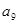 的等比中项
的等比中项
∴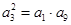 ,即
,即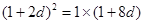 3分
3分
∵
∴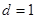 4分
4分
∴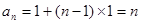 5分
5分
(2)由(1)可得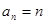 ,
,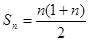 6分
6分
∴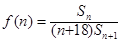
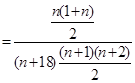
 8分
8分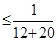
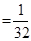 10分
10分
当且仅当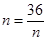 ,即
,即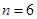 时,
时,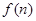 取得最大值
取得最大值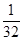 . 12分
. 12分
考点:1、等差数列概念、通项公式、前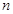 项和公式;2、等比中项的性质;3、基本不等式的应用.
项和公式;2、等比中项的性质;3、基本不等式的应用.

练习册系列答案
相关题目
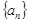 的前
的前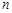 项和为
项和为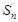 ,首项
,首项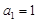 ,点
,点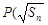 ,
,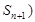 在曲线
在曲线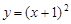 上.
上.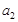 ,
,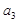 ;
;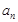 ;
;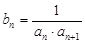 ,
,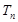 表示数列
表示数列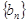 的前项和,若
的前项和,若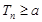 恒成立,求
恒成立,求 的取值范围.
的取值范围.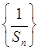 的前n项和,问是否存在常数m,使Tn=m
的前n项和,问是否存在常数m,使Tn=m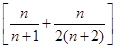 ,若存在,求m的值;若不存在,说明理由.
,若存在,求m的值;若不存在,说明理由.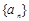 满足
满足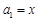 ,
,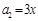 ,
,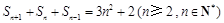 ,
,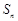 是数列
是数列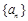 的前
的前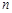 项和.
项和.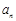 ;
;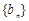 满足
满足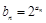 ,数列
,数列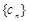 满足
满足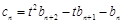 ,试比较数列
,试比较数列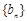 前
前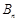 与
与 的大小;
的大小;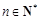 ,
,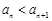 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. (a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;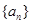 的前n项和为
的前n项和为 ,
, ,且
,且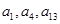 成等比数列.
成等比数列. ,求数列
,求数列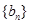 的前n项和.
的前n项和.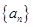 的前
的前 项和为
项和为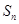 ,且
,且
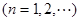 .
.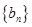 满足
满足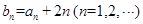 ,求数列
,求数列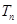 .
.