题目内容
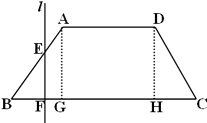
【题目】如图，已知底角为45°的等腰梯形ABCD，底边BC长为12，腰长为4 
，当一条垂直于底边BC（垂足为F）的直线l从左至右移动（与梯形ABCD有公共点）时，直线l把梯形分成两部分． 
（1）令BF=x（0＜x＜12），试写出直线右边部分的面积y与x的函数解析式；
（2）在（1）的条件下，令y=f（x）．构造函数g（x）= 
．
①判断函数g（x）在（4，8）上的单调性；
②判断函数g（x）在定义域内是否具有单调性，并说明理由．
【答案】
（1）解：过点A．D分别作AG⊥BC，DH⊥BC，垂足分别是G，H．
∵ABCD是等腰梯形，底角为45°，AB=4 
cm，
∴BG=AG=DH=HC=4cm，
又∵BC=12cm，
∴AD=GH=4cm，
①当点F在BG上时，
即x∈（0，4]时，f（x）=32﹣ 
x2；
②当点F在GH上时，
即x∈（4，8]时，f（x）=8+4（8﹣x）=40﹣4x．
③当点F在HC上时，
即x∈（8，12）时，y=S五边形ABFED=S梯形ACD﹣S三角形CEF
f（x）= （12﹣x）2，
∴函数解析式为f（x）= 
（2）解：g（x）=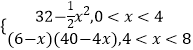 
，
①由二次函数的性质可知，函数g（x）在（4，8）上是减函数．
②虽然g（x）在（0，4）和（4，8）单调递减，
但是g（3.9）=24.395，g（4.1）=44.84，
∴g（3.9）＜g（4.1）．
因此函数g（x）在定义域内不具有单调性．
【解析】（1）可以通过分类讨论明确图形的特征，再根据图形形状求出函数的解析式；（2）可以求出函数g（x）的解析式，①由解析式即可得到判断函数的单调性，②分别求出g（3.9）=24.395，g（4.1）=44.84，比较即可．
练习册系列答案
考前必练系列答案
相关题目
