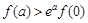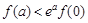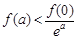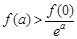题目内容
.(本题满分14分)
设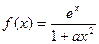 ,其中
,其中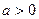
(Ⅰ)当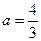 时,求
时,求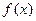 的极值点;
的极值点;
(Ⅱ)若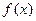 为R上的单调函数,求a的取值范围。
为R上的单调函数,求a的取值范围。
设
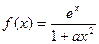 ,其中
,其中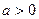
(Ⅰ)当
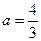 时,求
时,求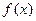 的极值点;
的极值点;(Ⅱ)若
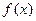 为R上的单调函数,求a的取值范围。
为R上的单调函数,求a的取值范围。解:对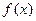 求导得
求导得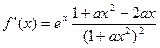 ①……………2分
①……………2分
(Ⅰ)当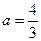 时,若
时,若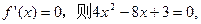
解得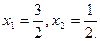 ……………4分
……………4分
综合①,可知
所以,
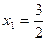 是极小值点,
是极小值点, 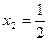 是极大值点. ……………8分
是极大值点. ……………8分
(II)若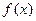 为R上的单调函数,则
为R上的单调函数,则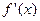 在R上不变号,
在R上不变号,
结 合①与条件a>0,知
合①与条件a>0,知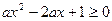 在R上恒成立,……………10分
在R上恒成立,……………10分
因此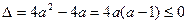 由此并结合
由此并结合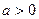 ,知
,知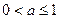 。
。
所以a的取值范围为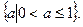 ……………14分
……………14分
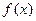 求导得
求导得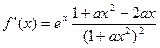 ①……………2分
①……………2分(Ⅰ)当
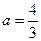 时,若
时,若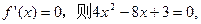
解得
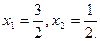 ……………4分
……………4分综合①,可知
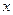 | 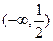 | 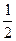 | 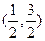 | 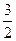 | 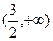 |
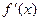 | + | 0 | - | 0 | + |
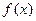 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以,

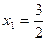 是极小值点,
是极小值点, 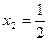 是极大值点. ……………8分
是极大值点. ……………8分(II)若
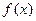 为R上的单调函数,则
为R上的单调函数,则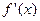 在R上不变号,
在R上不变号,结
 合①与条件a>0,知
合①与条件a>0,知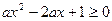 在R上恒成立,……………10分
在R上恒成立,……………10分因此
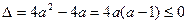 由此并结合
由此并结合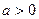 ,知
,知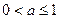 。
。所以a的取值范围为
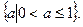 ……………14分
……………14分略

练习册系列答案
相关题目
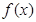 是定义在
是定义在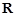 上的奇函数,且当
上的奇函数,且当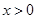 时,
时,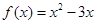 ,则
,则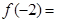 ( )
( )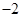
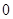
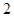
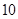
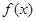 的图象如图所示,下列结论正确的是( )
的图象如图所示,下列结论正确的是( )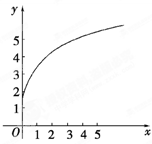
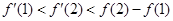
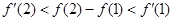
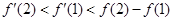
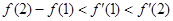
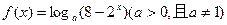
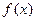 的反函数是其本身,求
的反函数是其本身,求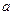 的值;
的值;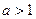 时,求函数
时,求函数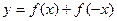 的最大值.
的最大值.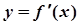 的图象,在标记的点中,函数有极小值的是 ( )
的图象,在标记的点中,函数有极小值的是 ( )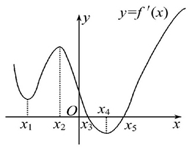
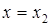
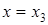
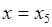

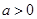 ,若
,若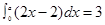 ,则
,则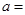
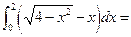 _________
_________ 在点
在点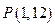 处的切线方程是
处的切线方程是 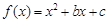 (
(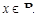 ),且满足
),且满足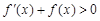 。对任意正实数a,下面不等式恒成立的是
。对任意正实数a,下面不等式恒成立的是