题目内容
已知函数 (
( 且
且 ).
).
(1)当 时,求证:
时,求证: 在
在 上单调递增;
上单调递增;
(2)当 且
且 时,求证:
时,求证: .
.
(1)证明如下(2)证明如下
解析试题分析:解:(1)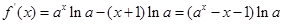
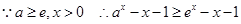
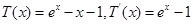
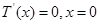
在 上
上 递减,在
递减,在 上
上 递增
递增
则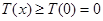
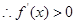
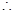
 在
在 上单调递增
上单调递增
(2)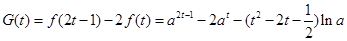
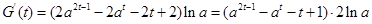
当 此时
此时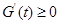
当 时,由(1)可知
时,由(1)可知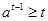
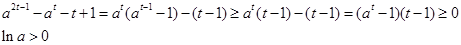
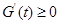
当 时,
时, 在
在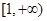 单调递增
单调递增
则
令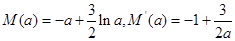
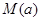 在
在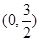 上单调递增,
上单调递增, 上单调递减
上单调递减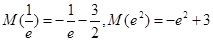
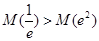
得证.
考点:导数的应用
点评:导数常应用于求曲线的切线方程、求函数的最值与单调区间、证明不等式和解不等式中参数的取值范围等。

练习册系列答案
相关题目
题目内容
已知函数 (
( 且
且 ).
).
(1)当 时,求证:
时,求证: 在
在 上单调递增;
上单调递增;
(2)当 且
且 时,求证:
时,求证: .
.
(1)证明如下(2)证明如下
解析试题分析:解:(1)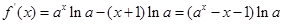
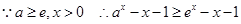
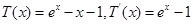
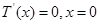
在 上
上 递减,在
递减,在 上
上 递增
递增
则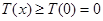
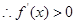
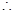
 在
在 上单调递增
上单调递增
(2)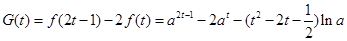
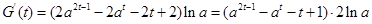
当 此时
此时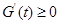
当 时,由(1)可知
时,由(1)可知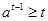
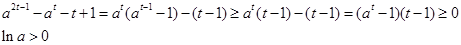
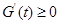
当 时,
时, 在
在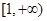 单调递增
单调递增
则
令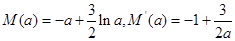
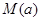 在
在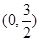 上单调递增,
上单调递增, 上单调递减
上单调递减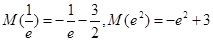
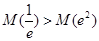
得证.
考点:导数的应用
点评:导数常应用于求曲线的切线方程、求函数的最值与单调区间、证明不等式和解不等式中参数的取值范围等。
