题目内容
【题目】已知 ,则方程
,则方程![]() 实数根的个数为 ( )
实数根的个数为 ( )
A. 7 B. 6 C. 5 D. 4
【答案】A
【解析】
由方程f[f(x)]=2先求出f(x)=1或f(x)=![]() 或f(x)=5,再解方程即可.
或f(x)=5,再解方程即可.
①当f(x)≤1时,
f[f(x)]=![]() =2,
=2,
解得,f(x)=1,
∴![]() =1或|log2(x﹣1)|=1,
=1或|log2(x﹣1)|=1,
∴x﹣1=![]() 或x﹣1=2,
或x﹣1=2,
故x=![]() 或x=3;
或x=3;
②若f(x)>1,则f[f(x)]=|log2(f(x)﹣1)|=2,
∴f(x)﹣1=![]() 或f(x)﹣1=4,
或f(x)﹣1=4,
∴f(x)=![]() 或f(x)=5,
或f(x)=5,
若f(x)=![]() ,则
,则![]() =
=![]() 或|log2(x﹣1)|=
或|log2(x﹣1)|=![]() ,
,
则x=﹣1或x=1+![]() 或x=1+
或x=1+![]() ;
;
若f(x)=5,则![]() =5或|log2(x﹣1)|=5,
=5或|log2(x﹣1)|=5,
则x=3(舍去)或x=1+2﹣5或x=1+25,
综上所述,方程f[f(x)]=2实数根的个数是7,
故答案为:A

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
(Ⅰ)在给定的坐标系中画出表中数据的散点图;

(Ⅱ)试对![]() 与
与![]() 的关系进行相关性检验,如
的关系进行相关性检验,如![]() 与
与![]() 具有线性相关关系,求出
具有线性相关关系,求出![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(Ⅲ)试预测加工![]() 个零件需要多少时间?
个零件需要多少时间?
参考数据:![]() ,
,![]() .
.
附: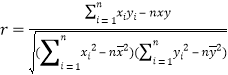 );
); ,
, ![]() ;
;
相关性检验的临界值表
n-2 | 小概率 | n-2 | 小概率 | n-2 | 小概率 | |||
0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | |||
1 | 0.997 | 1 | 4 | 0.811 | 0.917 | 7 | 0.666 | 0.798 |
2 | 0.950 | 0.990 | 5 | 0.754 | 0.874 | 8 | 0.632 | 0.765 |
3 | 0.878 | 0.959 | 6 | 0.707 | 0.834 | 9 | 0.602 | 0.735 |
注:表中的n为数据的组数
【题目】为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取顺序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() =
=![]() xi=9.97,s=
xi=9.97,s=![]() =
=![]() ≈0.212,
≈0.212,![]() ≈18.439,
≈18.439,![]() (xi﹣
(xi﹣![]() )(i﹣8.5)=﹣2.78,
)(i﹣8.5)=﹣2.78,
其中xi为抽取的第i个零件的尺寸,i=1,2,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产
过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地
变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在(![]() ﹣3s,
﹣3s,![]() +3s)之外的零件,就认为这条生产线在这一天
+3s)之外的零件,就认为这条生产线在这一天
的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①从这一天抽检的结果看,是否需对当天的生产过程进行检查?
②在(![]() ﹣3s,
﹣3s,![]() +3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的
均值与标准差.(精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=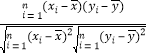 ,
,![]() ≈0.09.
≈0.09.