题目内容
【题目】如图,在正四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
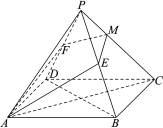
(1)求正四棱锥![]() 的全面积;
的全面积;
(2)若平面![]() 与棱
与棱![]() 交于点
交于点![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的大小(用反三角函数值表示).
所成锐二面角的大小(用反三角函数值表示).
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)根据正四棱锥的性质,用勾股定理求得侧面三角形的高,进而求得侧面积和底面积,即可得出答案.
(2)由题意,可建立空间直角坐标系,分别表示出平面![]() 与平面
与平面![]() 的法向量,求出两个法向量的夹角,即可得出答案.
的法向量,求出两个法向量的夹角,即可得出答案.
解:(1)因为正四棱锥![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,
![]() ,
,
![]()
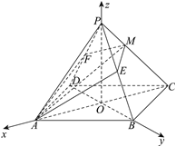
(2)连接![]() ,连接
,连接![]() ,记
,记![]() ,因为
,因为![]() ,
,![]() ,
,![]() 两两互相垂直
两两互相垂直
如图建立空间直角坐标系![]() .
.
因为![]() ,所以
,所以![]() .
.
所以![]()
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,所以
,所以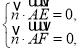 即
即![]()
所以![]() .令
.令![]() ,
,![]() ,所以
,所以![]() .
.
因为平面平面![]() 的一个法向量为
的一个法向量为![]()
设![]() 与
与![]() 的夹角为
的夹角为![]() ,
,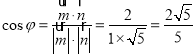
![]()
所以平面![]() 与平面
与平面![]() 所成锐二面角的大小是
所成锐二面角的大小是![]() .
.

【题目】某种植基地将编号分别为1,2,3,4,5,6的六个不同品种的马铃薯种在如图所示的
A | B | C | D | E | F |
这六块实验田上进行对比试验,要求这六块实验田分别种植不同品种的马铃薯,若种植时要求编号1,3,5的三个品种的马铃薯中至少有两个相邻,且2号品种的马铃薯不能种植在A、F这两块实验田上,则不同的种植方法有 ( )
A. 360种 B. 432种 C. 456种 D. 480种
【题目】汽车急刹车的停车距离与诸多因素有关,其中最为关键的两个因素是驾驶员的反应时间和汽车行驶的速度.设d表示停车距离,![]() 表示反应距离,
表示反应距离,![]() 表示制动距离,则
表示制动距离,则![]() .下图是根据美国公路局公布的试验数据制作的停车距离示意图,对应的汽车行驶的速度与停车距离的表格如下图所示
.下图是根据美国公路局公布的试验数据制作的停车距离示意图,对应的汽车行驶的速度与停车距离的表格如下图所示
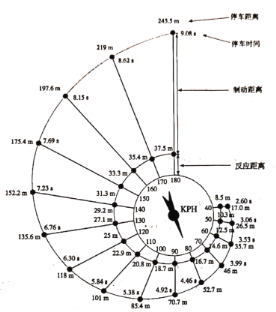
序号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格中的数据,建立停车距离与汽车速度的函数模型.可选择模型一:![]() 或模型二:
或模型二:![]() (其中v为汽车速度,a,b
(其中v为汽车速度,a,b
(2)通过计算![]() 时的停车距离,分析选择哪一个函数模型的拟合效果更好.
时的停车距离,分析选择哪一个函数模型的拟合效果更好.
(参考数据:![]() ;
;![]() ;
;![]() .)
.)
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位:千元/平方米)的统计数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于x的线性回归方程;
关于x的线性回归方程;
(2)利用(1)中的回归方程,分析2011年至2017年该市新开楼盘平均销售价格的变化情况,并预测该市2019年新开楼盘的平均销售价格。
附:参考公式:  ,
,![]() ,其中
,其中![]() 为样本平均值。
为样本平均值。
参考数据:![]()
![]() .
.
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好

