题目内容
11.已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=$\frac{5}{2}$cos($\frac{π}{2}$x)+log${\;}_{\frac{1}{2}}$x,则函数f(x)的零点个数为( )| A. | 4 | B. | 6 | C. | 7 | D. | 9 |
分析 作出当x>0时,f(x)=$\frac{5}{2}$cos($\frac{π}{2}$x)+log${\;}_{\frac{1}{2}}$x的图象,由图象解交点的个数,从而求零点的个数.
解答  解:当x>0时,函数f(x)=$\frac{5}{2}$cos($\frac{π}{2}$x)+lo${g}_{\frac{1}{2}}$x=$\frac{5}{2}$cos($\frac{π}{2}$x)-log2x的零点个数,
解:当x>0时,函数f(x)=$\frac{5}{2}$cos($\frac{π}{2}$x)+lo${g}_{\frac{1}{2}}$x=$\frac{5}{2}$cos($\frac{π}{2}$x)-log2x的零点个数,
即函数y=$\frac{5}{2}$cos($\frac{π}{2}$x)与函数y=log2x的交点个数,如图所示有3个交点,
又因为函数f(x)是定义在R上的奇函数,则f(0)=0,所以函数f(x)的零点个数为3×2+1=7.
故选:C.
点评 本题考查了函数的零点个数的判断,同时考查了数形结合的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.如图,在边长为e(e为自然对数的底数)的正方形中,阴影部分的面积为( )
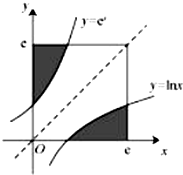

| A. | 2 | B. | $\frac{2}{e}$ | C. | e2 | D. | e |
2.已知函数f(x)=ex(x2+ax+1)在点(0,f(0))的切线与直线x-2y+6=0垂直,则a=( )
| A. | -3 | B. | -2 | C. | 2 | D. | 3 |
16.若函数f(x)=sin2ωπx(ω>0)的图象在区间[0,$\frac{1}{2}$]上至少有两个最高点,两个最低点,则ω的取值范围为( )
| A. | ω>2 | B. | ω≥2 | C. | ω>3 | D. | ω≥3 |