题目内容
1.(1)已知函数y=$\frac{1}{{x}^{2}-mx+1}$的定义域为R,求实数m的取值范围;(2)若关于x的不等式-x2-ax+a-3≤0在[-2,2]上恒成立.求实数a的取值范围.
分析 (1)由题意可得x2-mx+1≠0恒成立,即m2-4<0,解不等式即可得到m的范围;
(2)a(1-x)≤x2+3,对x讨论,当x=1时,当1<x≤2时,当-2≤x<1时,运用参数分离和对号函数的单调性,即可得到最值,解不等式可得a的范围.
解答 解:(1)函数y=$\frac{1}{{x}^{2}-mx+1}$的定义域为R,
即有x2-mx+1≠0恒成立,即m2-4<0,
解得-2<m<2,
则实数m的取值范围是(-2,2);
(2)关于x的不等式-x2-ax+a-3≤0在[-2,2]上恒成立,
即为a(1-x)≤x2+3,
当x=1时,0<3显然成立;
当1<x≤2时,-a≤$\frac{{x}^{2}+3}{x-1}$的最小值,
由x-1=t(0<t≤1),$\frac{{x}^{2}+3}{x-1}$=$\frac{(t+1)^{2}+3}{t}$=t+$\frac{4}{t}$+2在(0,1]递减,
t=1时,取得最小值,且为7,则-a≤7,
解得a≥-7;
当-2≤x<1时,-a≥$\frac{{x}^{2}+3}{x-1}$的最大值,
由x-1=t(-3≤t<0),$\frac{{x}^{2}+3}{x-1}$=$\frac{(t+1)^{2}+3}{t}$=t+$\frac{4}{t}$+2,
t=-2时,取得最大值,且为-2,则-a≥-2,
解得a≤2.
综上可得-7≤a≤2.
点评 本题考查函数的恒成立问题的求法,注意运用参数分离和单调性求最值,属于中档题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
11.已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=$\frac{5}{2}$cos($\frac{π}{2}$x)+log${\;}_{\frac{1}{2}}$x,则函数f(x)的零点个数为( )
| A. | 4 | B. | 6 | C. | 7 | D. | 9 |
6.如图,在三棱锥V-ABC,VA=VC,VB⊥AC,则AB与BC的大小关系是( )
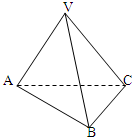

| A. | AB>BC | B. | AB=BC | C. | AB<BC | D. | 无法确定 |
13.已知函数f(x)=2cosx-$\frac{1}{x}$,若$\frac{π}{3}$<a<b<$\frac{5π}{6}$,则( )
| A. | f(a)>f(b) | B. | f(a)<f(b) | C. | f(a)=f(b) | D. | f(a)f(b)>0 |