题目内容
在平面直角坐标系xOy中，已知圆x2+y2=4上恰有两个点到直线4x-3y+c=0的距离为1，则实数c的取值范围是
（-15，-5）∪（5，15）
（-15，-5）∪（5，15）
．分析：由条件求出圆心，求出半径，由数形结合，只需圆心到直线的距离d大于半径与1的差小于半径与1的和即可．
解答：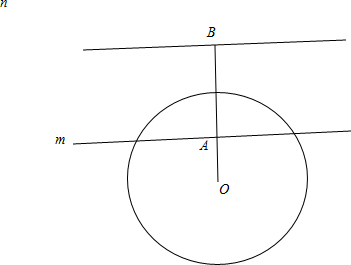
解：由已知可得：圆半径为2，圆心为（0，0）
故圆心（0，0）到直线4x-3y+c=0的距离为：d=
=
如图中的直线m恰好与圆由3个公共点，此时d=OA=2-1，
直线n与圆恰好有1个公共点，此时d=OB=2+1=3，当直线介于m、n之间满足题意．
故要使圆x2+y2=4上恰有两个点到直线4x-3y+c=0的距离为1，
只需d大于1小于3，即1＜
＜3，
解得：-15＜c＜-5，或5＜c＜15
故c的取值范围是：（-15，-5）∪（5，15））．
故答案为：（-15，-5）∪（5，15）
解：由已知可得：圆半径为2，圆心为（0，0）故圆心（0，0）到直线4x-3y+c=0的距离为：d=
| |c| | ||
|
| |c| |
| 5 |
如图中的直线m恰好与圆由3个公共点，此时d=OA=2-1，
直线n与圆恰好有1个公共点，此时d=OB=2+1=3，当直线介于m、n之间满足题意．
故要使圆x2+y2=4上恰有两个点到直线4x-3y+c=0的距离为1，
只需d大于1小于3，即1＜
| |c| |
| 5 |
解得：-15＜c＜-5，或5＜c＜15
故c的取值范围是：（-15，-5）∪（5，15））．
故答案为：（-15，-5）∪（5，15）
点评：本题考查圆与直线的位置关系，数形结合得出数量关系是解决问题的关键，属中档题．
练习册系列答案
习题精选系列答案
相关题目
如图，在平面直角坐标系xOy中，锐角α和钝角β的终边分别与单位圆交于A，B两点．若点A的横坐标是