Question

【题目】如图，在四棱锥中，平面，四边形为正方形，点分别为线段上的点，．

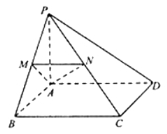
（1）求证：平面平面；

（2）求证：当点不与点重合时，平面；

（3）当，时，求点到直线距离的最小值．

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）．

【解析】

试题分析：（1）首先运用正方形的性质与线在垂直的性质定理推出平面，然后利用面面垂直的判定定理即可使问题得证；（2）结合（1）与已知条件可推出，由此根据线面平行的判定定理使问题得证；（3）根据条件可推出的长就是点到的距离，从而运用点到线的距离的计算，借助转化与化归的数学思想来求解．

试题解析：（1）证明：在正方形中，．

因为平面，平面，所以．

又，平面，所以平面．

因为平面，所以平面平面．

（2）证明：由（1）知，平面，平面，．

在中，，，所以，

又平面，平面，

所以平面．

（3）解：因为，所以平面，

而平面，所以，所以的长就是点到的距离，

而点在线段上，所以到直线距离的最小值是到线段的距离，

在中，，，所以到直线的最小值为．