题目内容
已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上截距相等,求切线的方程;
(2)若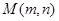 为圆C上任意一点,求
为圆C上任意一点,求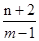 的最大值与最小值;
的最大值与最小值;
(3)从圆C外一点P(x,y)向圆引切线PM,M为切点,O为坐标原点,且有|PM|=|PO|,求当|PM|最小时的点P的坐标。
(1)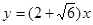 或
或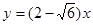 ;或
;或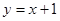 ,或
,或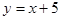 ;(2)最大值为-1,最小值为-7.;(3)当y=
;(2)最大值为-1,最小值为-7.;(3)当y=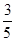 即P(
即P(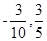 )时,|PM|最小.
)时,|PM|最小.
解析试题分析:(1)当截距为0时,设出切线方程为y=kx,同理列出关于k的方程,求出方程的解即可得到k的值,得到切线的方程;当截距不为零时,根据圆C的切线在x轴和y轴的截距相等,设出切线方程x+y=b,然后利用点到直线的距离公式求出圆心到切线的距离d,让d等于圆的半径r,列出关于b的方程,求出方程的解即可得到b的值,得到切线的方程;(2)设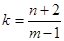 ,则
,则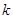 表示直线MA的斜率;其中A(1,-2)是定点;因为
表示直线MA的斜率;其中A(1,-2)是定点;因为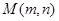 在圆C上,所以圆C与直线MA有公共点,而直线MA方程为:y+2=
在圆C上,所以圆C与直线MA有公共点,而直线MA方程为:y+2=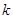 (x-1),则有:C点到直线MA的距离不大于圆C的半径,即:
(x-1),则有:C点到直线MA的距离不大于圆C的半径,即: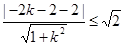 ,解得:
,解得: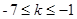 ,即可求出
,即可求出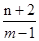 的最大值为和最小值;(3)根据圆切线垂直于过切点的半径,得到三角形CPM为直角三角形,根据勾股定理表示出点P的轨迹方程,由轨迹方程得到动点P的轨迹为一条直线,所以|PM|的最小值就是|PO|的最小值,求出原点到P轨迹方程的距离即为|PO|的最小值,然后利用两点间的距离公式表示出P到O的距离,把P代入动点的轨迹方程,两者联立即可此时P的坐标.
的最大值为和最小值;(3)根据圆切线垂直于过切点的半径,得到三角形CPM为直角三角形,根据勾股定理表示出点P的轨迹方程,由轨迹方程得到动点P的轨迹为一条直线,所以|PM|的最小值就是|PO|的最小值,求出原点到P轨迹方程的距离即为|PO|的最小值,然后利用两点间的距离公式表示出P到O的距离,把P代入动点的轨迹方程,两者联立即可此时P的坐标.
解:圆C的方程为:(x+1)2+(y-2)2=2
(1)圆C的切线在x轴和y轴上截距相等时,切线过原点或切线的斜率为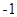 ;
;
当切线过原点时,设切线方程为:y=kx,相切则: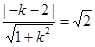 ,得
,得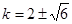 ;
;
当切线的斜率为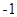 时,设切线方程为:y=-x+b,由相切得:
时,设切线方程为:y=-x+b,由相切得: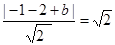 ,
,
得b=1或b=5;故所求切线方程为: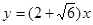 或
或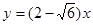 ;或
;或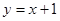 ,或
,或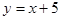
(2)设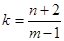 ,则
,则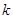 表示直线MA的斜率;其中A(1,-2)是定点;
表示直线MA的斜率;其中A(1,-2)是定点;
因为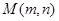 在圆C上,所以圆C与直线MA有公共点,
在圆C上,所以圆C与直线MA有公共点,
而直线MA方程为:y+2=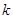 (x-1),则有:C点到直线MA的距离不大于圆C的半径
(x-1),则有:C点到直线MA的距离不大于圆C的半径
即: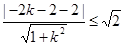 ,解得:
,解得: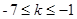 ,即
,即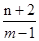 的最大值为-1,最小值为-7.
的最大值为-1,最小值为-7.
(3)由圆的切线长公式得|PM|2=|PC|2-R2=(x+1)2+(y-2)2-2;
由|PM|=|PO|得:(x+1)2+(y-2)2-2=x2+y2;即2x-4y+3=0, 即x=2y-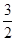
此时|PM|=|PO|=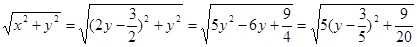
所以当y=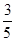 即P(
即P(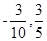 )时,|PM|最小.
)时,|PM|最小.
考点:1.直线的方程;2.直线与圆的位置关系.

 阅读快车系列答案
阅读快车系列答案 ,
, 是抛物线
是抛物线 的焦点,过点
的焦点,过点 与
与 、
、 两点,
两点, 为坐标原点.
为坐标原点. 为直径的圆的方程;
为直径的圆的方程; ,求直线
,求直线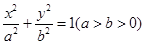 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率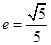 , 直线
, 直线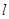 交椭圆于M,N两点.
交椭圆于M,N两点.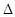 BMN的重心恰好为椭圆的右焦点F,求直线
BMN的重心恰好为椭圆的右焦点F,求直线 ,点
,点 依次满足
依次满足 。
。 的轨迹;
的轨迹;  作直线
作直线 交以
交以 为焦点的椭圆于
为焦点的椭圆于 两点,线段
两点,线段 的中点到
的中点到 轴的距离为
轴的距离为 ,且直线
,且直线 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点 及以
及以 都相切,如存在,求出
都相切,如存在,求出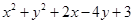 =0
=0 与圆C相切,且在
与圆C相切,且在 轴,
轴,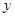 轴上的截距相等,求直线
轴上的截距相等,求直线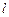 垂直的向量称为直线
垂直的向量称为直线 的一个法向量为
的一个法向量为 (1, ▲ )
(1, ▲ )